來源:登鏈社區
零知識證明在近 40 年中取得了顯著的發展,達到了前所未有的復雜性和效率水平。如今,每天都有新的論文和項目湧現,建立在豐富的思想和創新基礎之上。
想知道這一切是如何开始的嗎? 在這篇文章中,我們將深入探討零知識證明的歷史,探索 10 篇幫助塑造這一領域的裏程碑論文。
1 - 起源
Goldwasser, Micali, Rackoff - 交互式證明系統的知識復雜性 (1985) [^1]
我們的第一個裏程碑帶我們回到 1985 年那篇开創性的論文!這項工作引入了許多術語和基礎概念,這些概念至今仍然是零知識證明的核心。
首先,論文定義了一個證明系統,其模型爲一個涉及兩個概率圖靈機的雙方協議:一個證明者和一個驗證者。證明系統的目標是使證明者能夠說服驗證者某個給定輸入 x 屬於正式語言 L。在大多數早期工作中,證明者是計算上不受限制的,而驗證者則限制在多項式時間計算。在交互結束時,驗證者輸出“接受”或“拒絕”。

2 - 第一個應用
Fiat, Shamir - 如何證明自己:識別和籤名問題的實用解決方案 (1986) [^2]
這篇由 Fiat 和 Shamir 撰寫的論文,發表於零知識證明基礎工作的一年後,介紹了這些概念的第一個實際應用。他們提出了兩個協議:一個識別方案,這是交互式的,另一個是籤名方案,這是非交互式的。兩者之間的關鍵區別在於,在識別方案中,第三方可以通過制作有效的記錄來說服自己一個虛假的陳述。而在籤名協議中,即使是一個不誠實的證明者也無法說服自己一個虛假的陳述,從而使籤名不可僞造。
識別方案將二次剩余性證明系統應用爲交互式協議,其中驗證者發送隨機挑战,證明者相應地回應。籤名方案通過用對哈希函數的調用替換驗證者的挑战來修改這一點。
作者的名字聽起來熟悉嗎?這是一個強大通用技術的首次實例,現在被廣泛稱爲Fiat-Shamir 啓發式。它使得通過用對隨機預言機的查詢(在實踐中是加密哈希函數)替換驗證者的挑战,將任何公共幣交互式證明系統轉換爲非交互式的。
3 - 我們究竟能證明什么?
Goldreich, Micali, Wigderson - 如何在零知識中證明所有 NP 語句及密碼協議設計的方法論 (1987) [^3]
這篇 1986 年的論文給出了一個顯著的結果:每個 NP 中的語言都承認一個零知識證明系統。這很重要,因爲這意味着我們可以在不透露額外信息的情況下證明任何可以在多項式時間內驗證的陳述的真實性。作者通過提供一個圖的 3-着色性的證明系統來展示這一點,該問題是確定圖的節點是否可以用三種顏色着色,使得沒有兩個相鄰的節點共享相同的顏色。此外,證明僅假設存在概率加密。
證明的直覺如下:在每一輪中,
證明者選擇三種顏色的隨機排列, 證明者承諾每個節點的排列顏色, 驗證者查詢兩個相鄰節點並詢問它們的顏色, 證明者通過揭示查詢節點的顏色來打开承諾。 如果顏色匹配,驗證者立即拒絕。
通過以多項式次數運行此協議,驗證者以高概率確信證明者知道有效的 3-着色,而不學習任何信息,因爲打开的顏色在每一步都是隨機的!
在這項工作中還有兩篇其他論文同樣值得注意:所有可證明的內容都可以在零知識中證明[^4],該論文表明每個 IP 中的語言都有一個零知識證明系統,以及IP = PSPACE [^5],表明 IP 與 PSPACE 一樣強大。
4 - PCPs 和簡潔非交互式證明的起源
Micali - 計算上可靠的證明 (2000) [^6]
這篇 2000 年的論文由 Micali 撰寫,是零知識證明歷史上的一個重要貢獻。它甚至可以被視爲第一個 SNARK 構造,盡管當時尚未創造出 SNARK 這個術語!
Micali 的構造將任何概率可檢查證明(PCP)轉化爲簡潔且非交互式的證明。PCP 是可以通過僅閱讀少量位來驗證的證明,而一個關鍵結果,即PCP 定理 [^7],表明每個 NP 中的語言都有一個可以通過僅閱讀證明中的常數位來驗證的 PCP!
Micali 的構造使用默克爾樹如下:
證明者爲證明構建一個默克爾樹並將根發送給驗證者, 驗證者查詢他們希望檢查的特定位, 證明者提供這些位的認證路徑,驗證者驗證這些路徑。
通過簡單應用 Fiat-Shamir 啓發式,可以使該構造變爲非交互式(這種轉換的一個交互版本是由 Kilian 提出的 [^8])。論文還關注計算效率:實際上,驗證者不需要接收整個證明,而只需接收常數數量的位和認證路徑,這使得證明簡潔。該系統的主要缺點是 PCP 構造不切實際,這促使了交互式預言機證明(IOPs)的發展,IOPs 是 PCP 的一種推廣,可以產生實用的論證。
5 - 雙重高效的 IPs
Goldwasser, Kalai, Rothblum - 委托計算:針對麻瓜的交互式證明 (2015) [^9]
這篇論文強烈關注效率,並引入了廣爲人知的GKR 協議,這是一個針對可用算術電路的公共幣交互式協議。值得注意的是,驗證者和證明者都在多項式時間內運行,使其成爲雙重高效的交互式證明。
該協議开始於證明者和驗證者就一個輸入扇入爲 2 的算術電路達成一致。然後,證明者發送給定輸入值的電路聲稱輸出。協議通過逐層檢查電路進行,從輸出層开始,向輸入層移動。每一步將當前層的聲明減少爲對前一層的聲明,直到驗證者到達輸入層,在那裏他們可以檢查它是否與原始輸入匹配。
在每一步中,主要使用的原語是求和檢查協議 [^10],這是一種交互式證明,使證明者能夠說服驗證者關於一個具有 oracle 訪問權限的 v-變量多項式 g 的值之和,定義在布爾超立方體上:
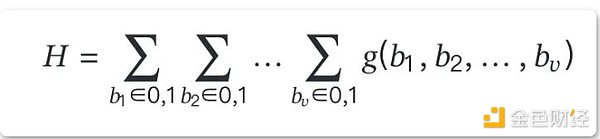
由於其高效性和簡單性,求和檢查協議和 GKR 協議在實踐中被廣泛使用。有關進一步的解釋,可以在 Thaler 的注釋中找到這些協議的替代概述 [^11]。
6 - 第一個實用的 SNARK
Gennaro, Gentry, Parno, Raykova - Quadratic Span Programs and Succinct NIZKs without PCPs (2013) [^12]
我們現在跳到一篇介紹第一個實用 SNARK 構造的論文!這項工作標志着旨在創建不依賴於低效 PCP 定理的 SNARK 研究的巔峰。雖然 PCP 定理提供了一個理論上的 SNARK 構造,但對於實際應用來說速度太慢,因此研究人員試圖尋找更高效的替代方案。例如,Groth 在 2010 年提出了一種基於雙线性群和配對的非交互式論證系統 [^13] ,盡管它需要證明者的二次時間。然而,這篇論文實現了线性證明者時間,代表了實際應用的重大改進。
這項工作爲其他重要協議鋪平了道路,例如Pinocchio 協議[^14] ,以及最終著名的Groth16[^15] 證明系統。該論文還介紹了二次跨度程序和二次算術程序,這些構造在這些系統中仍然至關重要。
這些構造的一個顯著缺點是需要可信設置,這意味着公共參考字符串生成階段產生的祕密信息(通常稱爲有毒廢物)如果不正確銷毀,可能會被用來創建虛假證明。此外,這種設置不是通用的,這意味着每個電路都需要新的設置。盡管存在這些限制,生成的證明大小在不同構造中仍然是最小的,使其成爲各種應用的熱門選擇。
還值得一提的是,Zerocash [^16] 的第一次迭代是一個早期且有影響力的區塊鏈應用,利用了 zk-SNARKs,建立在這些系統之上。
7 - PlonK SNARK
Gabizon, Williamson, Ciobotaru - PlonK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge (2019) [^17]
這篇 2019 年的影響力論文介紹了 PlonK SNARK,這是一個基於多項式交互式 oracle 證明(IOPs)的系統,這意味着驗證者可以對一些多項式進行 oracle 訪問,並可以在選擇的點上對其進行評估。該系統使用各種多項式小工具來證明關於多項式的陳述,其中最顯著的是大乘積論證,允許證明者表明在一個域上的評估的乘積爲 1。利用這一點,我們可以構造一個置換論證來證明兩個序列是彼此的置換。使用這些小工具,證明者可以爲任何算術電路構造證明,驗證者可以以非交互的方式驗證它。
在實踐中,oracle 訪問是通過多項式承諾方案(PCS)實現的,這允許證明者:
承諾一個多項式,並 提供在特定點評估該多項式的开放值。
這使得驗證者可以在任何點查詢多項式並驗證 IOP 的關系。論文中建議的 PCS 是KZG 承諾方案 [^18] ,它既高效又實用。KZG 使證明者對多項式的承諾作爲單個群元素,驗證者可以通過計算幾個橢圓曲线配對來確認开放值。雖然 KZG 需要可信設置,但它是通用的,可以在設置後用於任何電路。然而,PlonK 可以與其他 PCS 方案結合,使其適應透明論證系統。
此外,PlonK 中的置換論證啓發了查找論證。查找論證使證明者能夠表明一個序列的所有元素都包含在另一個序列中,這對於 zkVM 架構非常有用。查找論證允許將見證分解爲更小的軌跡,並證明它們之間的查找關系,從而使復雜證明更高效。
8 - STARKs
Ben-Sasson, Bentov, Horesh, Riabzev - Scalable, transparent, and post-quantum secure computational integrity (2018) [^19]
這篇論文介紹了 STARK 證明系統,另一種流行的證明系統,基於FRI [^20] ,這是一個用於 Reed-Solomon 碼的接近性測試的 IOP 協議。在 STARKs 中,證明者通過在一個域上構建默克爾樹來承諾多項式的評估。由於承諾的值最初是未知的,驗證者使用 FRI 確認這些評估形成一個足夠低度的有效多項式。該協議還可以作爲多項式承諾方案,允許驗證者檢查承諾多項式在任何點的評估。
STARKs 最引人注目的特點之一是它們僅依賴於密碼學抗碰撞哈希函數,而不是其他密碼學假設,如離散對數問題。這使得 STARKs 在潛在的後量子安全性方面具有優勢,因爲抗碰撞哈希函數被廣泛認爲即使在量子攻擊下也安全。此外,STARKs 是透明的,即它們不需要任何可信設置。它們也是通用的,這意味着它們不局限於特定電路,在各種應用中提供靈活性。
9 - 遞歸
Valiant - Incrementally verifiable computation or proofs of knowledge imply time/space efficiency. (2008) [^21]
多年來出現的一個重要概念是遞歸,簡單來說,這意味着一個證明可以用來證明另一個證明的正確性。本文中提出的場景涉及一個證明者希望證明一個可能很長的計算結果的正確性。給定一個圖靈機,我們可以證明狀態轉移函數的單個步驟的正確性,但這還不夠;我們想證明整個計算的正確性,這由一系列狀態轉移組成。
增量可驗證計算(IVC)背後的想法如下:假設我們可以證明從 S1 到 S2 的單個狀態轉移是正確的。然後,我們可以將兩個證明合並爲一個:證明者表明他們知道兩個有效證明:

合並的證明將說服驗證者從 S1 到 S3 的轉移是正確的。這個過程可以對任意數量的步驟重復,使我們能夠將任意長的計算壓縮爲一個證明(更具體地說,是多項式長的計算)。
重要的是要注意,這個構造依賴於兩個關鍵假設:
證明系統的知識健全性:證明者不僅必須證明單個狀態轉換的證明存在,還必須證明他們知道這些證明。直觀上講,通過歸納的知識可提取性,我們可以提取所有單個狀態轉換的證明。 實際中的哈希函數是隨機預言機:這是一個更強的假設,但對於驗證聚合證明中子證明的正確性是必要的。
盡管這個構造在理論上是強大的,但在實踐中應用成本高。爲了解決這個問題,提出了新的方法來提高效率。其中之一是使用折疊方案 [^22] ,它放寬了假設並避免了遞歸 SNARK 驗證的需要。折疊的想法是,給定兩個證明,π 和 π′,我們可以將它們“折疊”成一個單一的證明,π″。驗證者相信,如果折疊實例是可滿足的,則原始實例也是可滿足的。
10 - 通過 zkVM 進行可驗證計算
Ben-Sasson, Chiesa, Tromer, Virza - 適用於馮·諾依曼架構的簡潔非交互式零知識 (2014) [^23]
這篇最終的論文討論了第一個實用的 零知識虛擬機 (zkVM) 構造,這是一種能夠執行任意程序並生成這些計算正確性證明的虛擬機。所描述的機器遵循馮·諾依曼架構,這意味着程序和數據存儲在同一內存中。大多數現代 CPU 基於這一範式,因此,從理論上講,任何可以在經典計算機上運行的程序也可以在該架構上運行。
論文介紹了一種稱爲 vnTinyRAM 的 RISC 架構,並展示了一個移植到該指令集的 C 編譯器。證明系統旨在驗證程序執行的正確性,直到固定的步驟數爲止。其基本思想是電路被構造爲一個重復的狀態轉換函數,展开直到達到指令計數限制。
如今,zkVM 越來越受歡迎。它們的一個關鍵優勢是用戶可以使用 高級編程語言 編寫程序並用它們生成證明。這相較於手動編寫電路提供了顯著的優勢,因爲許多標准算法和數據結構已經在這些高級語言中定義。此外,开發者可以重用熟悉的計算模型,這大大降低了使用零知識證明的學習曲线。
還值得注意的是,許多 zk-rollup 基於這一模型。例如,支持以太坊虛擬機 (EVM) 執行的 zk-rollup 使用 zkVM 來證明 EVM 執行的正確性。
最後,論文介紹了其自身的架構,優化用於零知識證明系統。另一個流行的 zk 友好架構示例是 Cairo CPU 架構 [^24] ,這是一個經過優化以使用 STARKs 進行證明的圖靈完備 CPU。
參考論文
[^1]: Goldwasser, S., Micali, S., & Rackoff, C. (1985). The knowledge complexity of interactive proof-systems. (link) ↩︎
[^2]: Fiat, A., & Shamir, A. (1986). How to prove yourself: Practical solutions to identification and signature problems. (link) ↩︎
[^3]: Goldreich, O., Micali, S., & Wigderson, A. (1987). How to prove all NP statements in zero-knowledge and a methodology of cryptographic protocol design. (link) ↩︎
[^4]: Ben-Or, M., Goldreich, O., Goldwasser, S., Håstad, J., Kilian, J., Micali, S., & Rogaway, P. (1990). Everything provable is provable in zero-knowledge. (link) ↩︎
[^5]: Shamir, A. (1992). IP=PSPACE. (link) ↩︎
[^6]: Micali, S. (2000). Computationally sound proofs. ([link](https://people.csail.mit.edu/silvio/Selected Scientific Papers/Proof Systems/Computationally_Sound_Proofs.pdf)) ↩︎
[^7]: Cook, S. A. (1971). Proof Verification and Hardness of Approximation Problems. (link) ↩︎
[^8]: Kilian, J. (1992, July). A note on efficient zero-knowledge proofs and arguments. (link) ↩︎
[^9]: Goldwasser, S., Kalai, Y. T., & Rothblum, G. N. (2015). Delegating computation: interactive proofs for muggles. (link, see also this note by Justin Thaler) ↩︎
[^10]: Lund, C., Fortnow, L., Karloff, H., & Nisan, N. (1992). Algebraic methods for interactive proof systems. (link) ↩︎
[^11]: Thaler, J. (2015). A note on the GKR protocol. (link) ↩︎
[^12]: Gennaro, R., Gentry, C., Parno, B., & Raykova, M. (2013). Quadratic span programs and succinct NIZKs without PCPs. (link) ↩︎
[^13]: Groth, J. (2010). Short pairing-based non-interactive zero-knowledge arguments. (link) ↩︎
[^14]: Parno, B., Howell, J., Gentry, C., & Raykova, M. (2016). Pinocchio: Nearly practical verifiable computation. (link) ↩︎
[^15]: Groth, J. (2016). On the size of pairing-based non-interactive arguments. (link) ↩︎
[^16]: Sasson, E. B., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer, E., & Virza, M. (2014). Zerocash: Decentralized anonymous payments from bitcoin. (link) ↩︎
[^17]: Gabizon, A., Williamson, Z. J., & Ciobotaru, O. (2019). Plonk: Permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge. (link) ↩︎
[^18]: Kate, A., Zaverucha, G. M., & Goldberg, I. (2010). Constant-size commitments to polynomials and their applications. (link) ↩︎
[^19]: Ben-Sasson, E., Bentov, I., Horesh, Y., & Riabzev, M. (2018). Scalable, transparent, and post-quantum secure computational integrity. (link) ↩︎
[^20]: Ben-Sasson, E., Bentov, I., Horesh, Y., & Riabzev, M. (2018). Fast reed-solomon interactive oracle proofs of proximity. (link) ↩︎
[^21]: Valiant, P. (2008). Incrementally verifiable computation or proofs of knowledge imply time/space efficiency. (link) ↩︎
[^22]: Kothapalli, A., Setty, S., & Tzialla, I. (2022, August). Nova: Recursive zero-knowledge arguments from folding schemes. (link) ↩︎
[^23]: Ben-Sasson, E., Chiesa, A., Tromer, E., & Virza, M. (2014). Succinct Non-Interactive zero knowledge for a von neumann architecture. (link) ↩︎
[^24]: Goldberg, L., Papini, S., & Riabzev, M. (2021). Cairo–a Turing-complete STARK-friendly CPU architecture. (link) ↩︎
鄭重聲明:本文版權歸原作者所有,轉載文章僅為傳播信息之目的,不構成任何投資建議,如有侵權行為,請第一時間聯絡我們修改或刪除,多謝。
