
在關於零知識證明的先進形式化驗證的系列博客中,我們已經討論了如何驗證 ZK 指令以及對兩個 ZK 漏洞的深度剖析。正如在公开報告和代碼庫中所顯示的,通過形式化驗證每一條 zkWasm 指令,我們找到並修復了每一個漏洞,從而能夠完全驗證整個 zkWasm 電路的技術安全性和正確性。
盡管我們已展示了驗證一條 zkWasm 指令的過程,並介紹了相關的項目初步概念,但熟悉形式化驗證讀者可能更想了解 zkVM 與其他較小的 ZK 系統、或其他類型的字節碼 VM 在驗證上的獨特之處。在本文中,我們將深入討論在驗證 zkWasm 內存子系統時所遇到的一些技術要點。內存是 zkVM 最爲獨特的部分,處理好這一點對所有其他 zkVM 的驗證都至關重要。
形式化驗證:虛擬機(VM)對 ZK 虛擬機(zkVM)
我們的最終目標是驗證 zkWasm 的正確性,其與普通的字節碼解釋器(VM,例如以太坊節點所使用的 EVM 解釋器)的正確性定理相似。亦即,解釋器的每一執行步驟都與基於該語言操作語義的合法步驟相對應。如下圖所示,如果字節碼解釋器的數據結構當前狀態爲 SL,且該狀態在 Wasm 機器的高級規範中被標記爲狀態 SH,那么當解釋器步進到狀態 SL'時,必須存在一個對應的合法高級狀態 SH',且 Wasm 規範中規定了 SH 必須步進到 SH'。
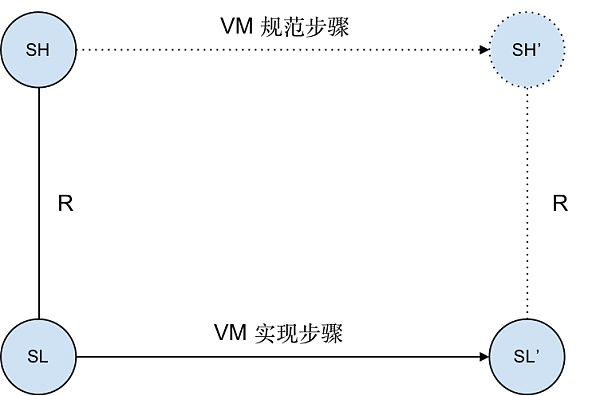
同樣地,zkVM 也有一個類似的正確性定理:zkWasm 執行表中新的每一行都與一個基於該語言操作語義的合法步驟相對應。如下圖所示,如果執行表中某行數據結構的當前狀態是 SR,且該狀態在 Wasm 機器的高級規範中表示爲狀態 SH,那么執行表的下一行狀態 SR'必須對應一個高級狀態 SH',且 Wasm 規範中規定了 SH 必須步進到 SH'。
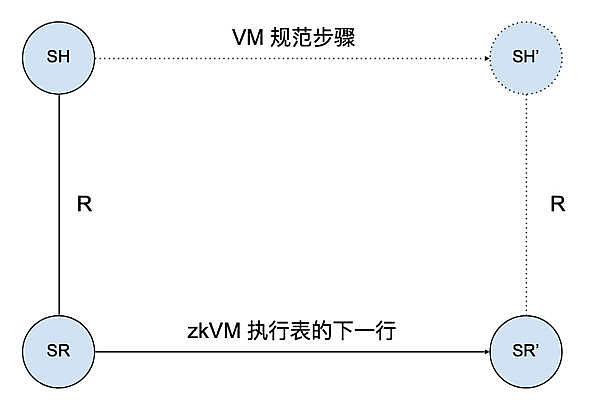
由此可見,無論是在 VM 還是 zkVM 中,高級狀態和 Wasm 步驟的規範是一致的,因此可以借鑑先前對編程語言解釋器或編譯器的驗證經驗。而 zkVM 驗證的特殊之處在於其構成系統低級狀態的數據結構類型。
首先,如我們在之前的博客文章中所述,zk 證明器在本質上是對大素數取模的整數運算,而 Wasm 規範和普通解釋器處理的是 32 位或 64 位整數。zkVM 實現的大部分內容都涉及到此,因此,在驗證中也需要做相應的處理。然而,這是一個“本地局部”問題:因爲需要處理算術運算,每行代碼變得更復雜,但代碼和證明的整體結構並沒有改變。
另一個主要的區別是如何處理動態大小的數據結構。在常規的字節碼解釋器中,內存、數據棧和調用棧都被實現爲可變數據結構,同樣的,Wasm 規範將內存表示爲具有 get/set 方法的數據類型。例如,Geth 的 EVM 解釋器有一個`Memory`數據類型,它被實現爲表示物理內存的字節數組,並通過`Set 32 `和`GetPtr`方法寫入和讀取。爲了實現一條內存存儲指令,Geth 調用`Set 32 `來修改物理內存。
func opMstore(pc *uint 64, interpreter *EVMInterpreter, scope *ScopeContext) ([]byte, error) {
// pop value of the stack
mStart, val := scope.Stack.pop(), scope.Stack.pop()
scope.Memory.Set 32(mStart.Uint 64(), &val)
return nil, nil
}
在上述解釋器的正確性證明中,我們在對解釋器中的具體內存和在規範中的抽象內存進行賦值之後,證明其高級狀態和低級狀態相互匹配,這相對來說是比較容易的。
然而,對於 zkVM 而言,情況將變得更加復雜。
zkWasm 的內存表和內存抽象層
在 zkVM 中,執行表上有用於固定大小數據的列(類似於 CPU 中的寄存器),但它不能用來處理動態大小的數據結構,這些數據結構要通過查找輔助表來實現。zkWasm 的執行表有一個 EID 列,該列的取值爲 1、 2、 3 ……,並且有內存表和跳轉表兩個輔助表,分別用於表示內存數據和調用棧。
以下是一個提款程序的實現示例:
int balance, amount;
void main () {
balance = 100;
amount = 10;
balance -= amount; // withdraw
}
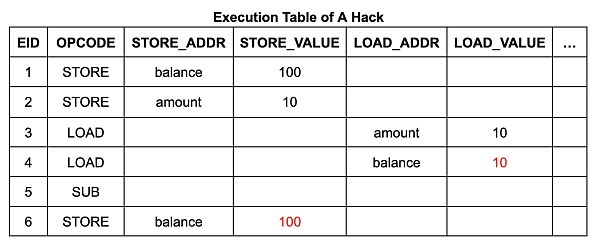
執行表的內容和結構相當簡單。它有 6 個執行步驟(EID 1 到 6),每個步驟都有一行列出其操作碼(opcode),如果該指令是內存讀取或寫入,則還會列出其地址和數據:
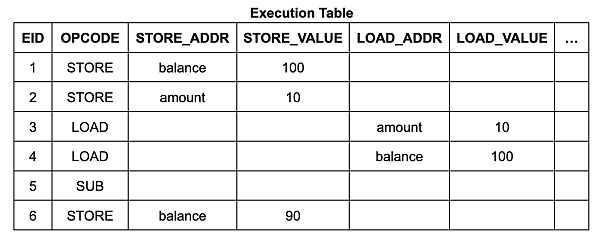
內存表中的每一行都包含地址、數據、起始 EID 和終止 EID。起始 EID 是寫入該數據到該地址的執行步驟的 EID,終止 EID 是下一個將會寫入該地址的執行步驟的 EID。(它還包含一個計數,我們稍後詳細討論。)對於 Wasm 內存讀取指令電路,其使用查找約束來確保表中存在一個合適的表項,使得讀取指令的 EID 在起始到終止的範圍內。(類似地,跳轉表的每一行對應於調用棧的一幀,每行均標有創建它的調用指令步驟的 EID。)
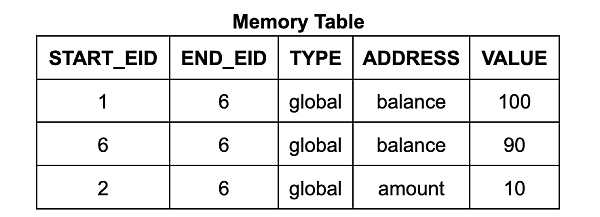
這個內存系統與常規 VM 解釋器的區別很大:內存表不是逐步更新的可變內存,而是包含整個執行軌跡中所有內存訪問的歷史記錄。爲了簡化程序員的工作,zkWasm 提供了一個抽象層,通過兩個便捷入口函數來實現。分別是:
alloc_memory_table_lookup_write_cell
和
Alloc_memory_table_lookup_read_cell
其參數如下:

例如,zkWasm 中實現內存存儲指令的代碼包含了一次對’write alloc’函數的調用:
let memory_table_lookup_heap_write1 = allocator
.alloc_memory_table_lookup_write_cell_with_value(
"store write res 1",
constraint_builder,
eid,
move |____| constant_from!(LocationType::Heap as u 64),
move |meta| load_block_index.expr(meta), // address
move |____| constant_from!( 0), // is 32-bit
move |____| constant_from!( 1), // (always) enabled
);
let store_value_in_heap1 = memory_table_lookup_heap_write1.value_cell;
`alloc`函數負責處理表之間的查找約束以及將當前`eid`與內存表條目相關聯的算術約束。由此,程序員可以將這些表看作普通內存,並且在代碼執行之後 `store_value_in_heap1`的值已被賦給了`load_block_index` 地址。
類似地,內存讀取指令使用`read_alloc`函數實現。在上面的示例執行序列中,每條加載指令有一個讀取約束,每條存儲指令有一個寫入約束,每個約束都由內存表中的一個條目所滿足。
mtable_lookup_write(row 1.eid, row 1.store_addr, row 1.store_value)
⇐ (row 1.eid= 1 ∧ row 1.store_addr=balance ∧ row 1.store_value= 100 ∧ ...)
mtable_lookup_write(row 2.eid, row 2.store_addr, row 2.store_value)
⇐ (row 2.eid= 2 ∧ row 2.store_addr=amount ∧ row 2.store_value= 10 ∧ ...)
mtable_lookup_read(row 3.eid, row 3.load_addr, row 3.load_value)
⇐ ( 2<row 3.eid≤ 6 ∧ row 3.load_addr=amount ∧ row 3.load_value= 100 ∧ ...)
mtable_lookup_read(row 4.eid, row 4.load_addr, row 4.load_value)
⇐ ( 1<row 4.eid≤ 6 ∧ row 4.load_addr=balance ∧ row 4.load_value= 10 ∧ ...)
mtable_lookup_write(row 6.eid, row 6.store_addr, row 6.store_value)
⇐ (row 6.eid= 6 ∧ row 6.store_addr=balance ∧ row 6.store_value= 90 ∧ ...)
形式化驗證的結構應與被驗證軟件中所使用的抽象相對應,使得證明可以遵循與代碼相同的邏輯。對於 zkWasm,這意味着我們需要將內存表電路和“alloc read/write cell”函數作爲一個模塊來進行驗證,其接口則像可變內存。給定這樣的接口後,每條指令電路的驗證可以以類似於常規解釋器的方式進行,而額外的 ZK 復雜性則被封裝在內存子系統模塊中。
在驗證中,我們具體實現了“內存表其實可以被看作是一個可變數據結構”這個想法。亦即,編寫函數 `memory_at type`,其完整掃描內存表、並構建相應的地址數據映射。(這裏變量 `type` 的取值範圍爲三種不同類型的 Wasm 內存數據:堆、數據棧和全局變量。)而後,我們證明由 alloc 函數所生成的內存約束等價於使用 set 和 get 函數對相應地址數據映射所進行的數據變更。我們可以證明:
對於每一 eid,如果以下約束成立
memory_table_lookup_read_cell eid type offset value
則
get (memory_at eid type) offset = Some value
並且,如果以下約束成立
memory_table_lookup_write_cell eid type offset value
則
memory_at (eid+ 1) type = set (memory_at eid type) offset value
在此之後,每條指令的驗證可以建立在對地址數據映射的 get 和 set 操作之上,這與非 ZK 字節碼解釋器相類似。
zkWasm 的內存寫入計數機制
不過,上述的簡化描述並未揭示內存表和跳轉表的全部內容。在 zkVM 的框架下,這些表可能會受到攻擊者的操控,攻擊者可以輕易地通過插入一行數據來操縱內存加載指令,返回任意數值。
以提款程序爲例,攻擊者有機會在提款操作前,通過僞造一個$ 110 的內存寫入操作,將虛假數據注入到账戶余額中。這一過程可以通過在內存表中添加一行數據,並修改內存表和執行表中現有單元格的數值來實現。這將導致其可以進行“免費”的提款操作,因爲账戶余額在操作後將仍然保持在$ 100 。
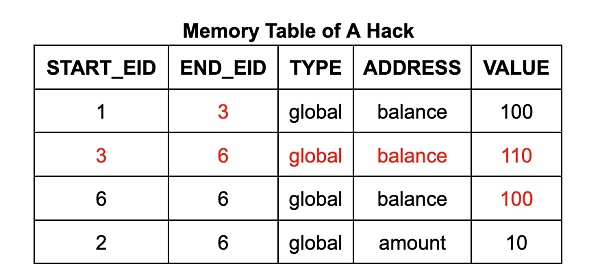
爲確保內存表(和跳轉表)僅包含由實際執行的內存寫入(和調用及返回)指令生成的有效條目,zkWasm 採用了一種特殊的計數機制來監控條目數量。具體來說,內存表設有一個專門的列,用以持續追蹤內存寫入條目的總數。同時,執行表中也包含了一個計數器,用於統計每個指令預期進行的內存寫入操作的次數。通過設置一個相等約束,從而確保這兩個計數是一致的。這種方法的邏輯十分直觀:每當內存進行寫入操作,就會被計數一次,而內存表中相應地也應有一條記錄。因此,攻擊者無法在內存表中插入任何額外的條目。
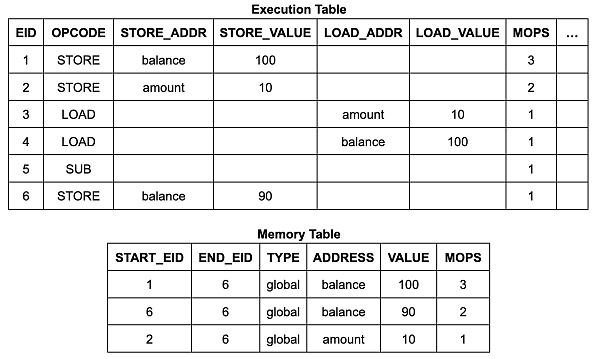
上面的邏輯陳述有點模糊,在機械化證明的過程中,需要使其更加精確。首先,我們需要修正前述內存寫入引理的陳述。我們定義函數`mops_at eid type`,對具有給定`eid`和`type`的內存表條目計數(大多數指令將在一個 eid 處創建 0 或 1 個條目)。該定理的完整陳述有一個額外的前提條件,指出沒有虛假的內存表條目:
如果以下約束成立
(memory_table_lookup_write_cell eid type offset value)
並且以下新增約束成立
(mops_at eid type) = 1
則
(memory_at(eid+ 1) type) = set (memory_at eid type) offset value
這要求我們的驗證比前述情況更精確。 僅僅從相等約束條件中得出內存表條目總數等於執行中的總內存寫入次數並不足以完成驗證。爲了證明指令的正確性,我們需要知道每條指令對應了正確數目的內存表條目。例如,我們需要排除攻擊者是否可能在執行序列中略去某條指令的內存表條目,並爲另一條無關指令創建一個惡意的新內存表條目。
爲了證明這一點,我們採用了由上至下的方式,對給定指令對應的內存表條目數量進行限制,這包括了三個步驟。首先,我們根據指令類型爲執行序列中的指令預估了所應該創建的條目數量。我們稱從第 i 個步驟到執行結束的預期寫入次數爲`instructions_mops i`,並稱從第 i 條指令到執行結束在內存表中的相應條目數爲`cum_mops (eid i)`。通過分析每條指令的查找約束,我們可以證明其所創建的條目不少於預期,從而可以得出所跟蹤的每一段 [i... numRows] 所創建的條目不少於預期:
Lemma cum_mops_bound': forall n i,
0 ≤ i ->
i + Z.of_nat n = etable_numRow ->
MTable.cum_mops (etable_values eid_cell i) (max_eid+ 1) ≥ instructions_mops' i n.
其次,如果能證明表中的條目數不多於預期,那么它就恰好具有正確數量的條目,而這一點是顯而易見的。
Lemma cum_mops_equal' : forall n i,
0 ≤ i ->
i + Z.of_nat n = etable_numRow ->
MTable.cum_mops (etable_values eid_cell i) (max_eid+ 1) ≤ instructions_mops' i n ->
MTable.cum_mops (etable_values eid_cell i) (max_eid+ 1) = instructions_mops' i n.
現在進行第三步。我們的正確性定理聲明:對於任意 n,cum_mops 和 instructions_mops 在表中從第 n 行到末尾的部分總是一致的:
Lemma cum_mops_equal : forall n,
0 <= Z.of_nat n < etable_numRow ->
MTable.cum_mops (etable_values eid_cell (Z.of_nat n)) (max_eid+ 1) = instructions_mops (Z.of_nat n)
通過對 n 進行歸納總結來完成驗證。表中的第一行是 zkWasm 的等式約束,表明內存表中條目的總數是正確的,即 cum_mops 0 = instructions_mops 0 。對於接下來的行,歸納假設告訴我們:
cum_mops n = instructions_mops n
並且我們希望證明
cum_mops (n+ 1) = instructions_mops (n+ 1)
注意此處
cum_mops n = mop_at n + cum_mops (n+ 1)
並且
instructions_mops n = instruction_mops n + instructions_mops (n+ 1)
因此,我們可以得到
mops_at n + cum_mops (n+ 1) = instruction_mops n + instructions_mops (n+ 1)
此前,我們已經證明了每條指令將創造不少於預期數量的條目,例如
mops_at n ≥ instruction_mops n.
所以可以得出
cum_mops (n+ 1) ≤ instructions_mops (n+ 1)
這裏我們需要應用上述第二個引理。
(用類似的引理對跳轉表進行驗證,可證得每條調用指令都能准確地產生一個跳轉表條目,這個證明技術因此普遍適用。然而,我們仍需要進一步的驗證工作來證明返回指令的正確性。返回的 eid 與創建調用幀的調用指令的 eid 是不同的,因此我們還需要一個附加的不變性質,用來聲明 eid 數值在執行序列中是單向遞增的。)
如此詳細地說明證明過程,是形式化驗證的典型特徵,也是驗證特定代碼片段通常比編寫它需要更長時間的原因。然而這樣做是否值得?在這裏的情況下是值得的,因爲我們在證明的過程中的確發現了一個跳轉表計數機制的關鍵錯誤。之前的文章中已經詳細描述了這個錯誤——總結來說,舊版本的代碼同時計入了調用和返回指令,而攻擊者可以通過在執行序列中添加額外的返回指令,來爲僞造的跳轉表條目騰出空間。盡管不正確的計數機制可以滿足對每條調用和返回指令都計數的直覺,但當我們試圖將這種直覺細化爲更精確的定理陳述時,問題就會凸顯出來。
使證明過程模塊化
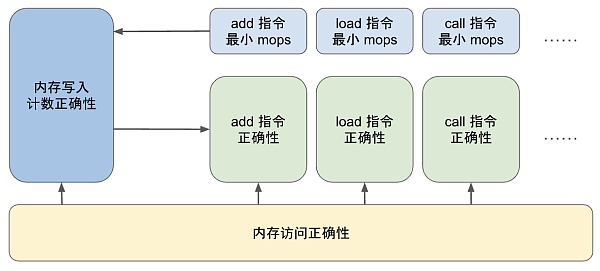
從上面的討論中,我們可以看到在關於每條指令電路的證明和關於執行表的計數列的證明之間存在着一種循環依賴關系。要證明指令電路的正確性,我們需要對其中的內存寫入進行推理;即需要知道在特定 EID 處內存表條目的數量、以及需要證明執行表中的內存寫入操作計數是正確的;而這又需要證明每條指令至少執行了最少數量的內存寫入操作。
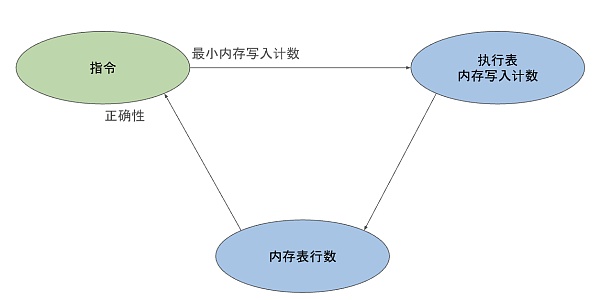
此外,還有一個需要考慮的因素,zkWasm 項目相當龐大,因此驗證工作需要模塊化,以便多位驗證工程師分工處理。因此,對計數機制的證明解構時需要特別注意其復雜性。例如,對於 LocalGet 指令,有兩個定理如下:
Theorem opcode_mops_correct_local_get : forall i,
0 <= i ->
etable_values eid_cell i > 0 ->
opcode_mops_correct LocalGet i.
Theorem LocalGetOp_correct : forall i st y xs,
0 <= i ->
etable_values enabled_cell i = 1 ->
mops_at_correct i ->
etable_values (ops_cell LocalGet) i = 1 ->
state_rel i st ->
wasm_stack st = xs ->
(etable_values offset_cell i) > 1 ->
nth_error xs (Z.to_nat (etable_values offset_cell i - 1)) = Some y ->
state_rel (i+ 1) (update_stack (incr_iid st) (y :: xs)).
第一個定理聲明
opcode_mops_correct LocalGet i
展开定義後,意味着該指令在第 i 行至少創建了一個內存表條目(數字 1 是在 zkWasm 的 LocalGet 操作碼規範中指定的)。
第二個定理是該指令的完整正確性定理,它引用
mops_at_correct i
作爲假設,這意味着該指令准確地創建了一個內存表條目。
驗證工程師可以分別獨立地證明這兩個定理,然後將它們與關於執行表的證明結合起來,從而證得整個系統的正確性。值得注意的是,所有針對單個指令的證明都可以在讀取/寫入約束的層面上進行,而無須了解內存表的具體實現。因此,項目分爲三個可以獨立處理的部分。
總結
逐行驗證 zkVM 的電路與驗證其他領域的 ZK 應用並沒有本質區別,因爲它們都需要對算術約束進行類似的推理。從高層來看,對 zkVM 的驗證需要用到許多運用於編程語言解釋器和編譯器形式化驗證的方法。這裏主要的區別在於動態大小的虛擬機狀態。然而,通過精心構建驗證結構來匹配實現中所使用的抽象層,這些差異的影響可以被最小化,從而使得每條指令都可以像對常規解釋器那樣,基於 get-set 接口來進行獨立的模塊化驗證。
鄭重聲明:本文版權歸原作者所有,轉載文章僅為傳播信息之目的,不構成任何投資建議,如有侵權行為,請第一時間聯絡我們修改或刪除,多謝。
