作者:以太坊創始人Vitalik;編譯:鄧通,金色財經
按:本文爲以太坊創始人Vitalik近期發表的“以太坊協議的未來發展”系列文章的第四部分“Possible futures of the Ethereum protocol, part 4: The Verge”。第三部分見“Vitalik:以太坊The Scourge階段的關鍵目標”,第二部分見“Vitalik:The Surge階段以太坊協議應該怎么發展”,第一部分見“以太坊PoS還有哪些可以改進”。以下爲第四部分全文:
特別感謝 Justin Drake、Hsiao-wei Wang、Guillaume Ballet、Ignacio、Josh Rudolf、Lev Soukhanov、Ryan Sean Adams 和 Uma Roy 的反饋和審查。
區塊鏈最強大的功能之一是任何人都可以在自己的計算機上運行節點並驗證鏈是否正確。即使運行鏈上共識(PoW、PoS……)的95%的節點都立即同意改變規則,並开始按照新規則生產區塊,每個運行完全驗證節點的人都會拒絕接受這條鏈。 不屬於此類集團的利益相關者將自動匯聚並繼續構建一條繼續遵循舊規則的鏈,並且完全驗證的用戶將遵循該鏈。
這是區塊鏈和中心化系統之間的關鍵區別。然而,爲了保持這一特性,運行完全驗證的節點需要對臨界數量的人來說實際上是可行的。這既適用於質押者(就好像質押者沒有驗證鏈,他們實際上並沒有爲執行協議規則做出貢獻),也適用於普通用戶。如今,可以在消費類筆記本電腦(包括用於撰寫本文的筆記本電腦)上運行節點,但這樣做很困難。 The Verge 旨在改變這一現狀,讓完全驗證鏈的計算成本變得如此低廉,以至於每個移動錢包、瀏覽器錢包,甚至智能手表都默認這樣做。
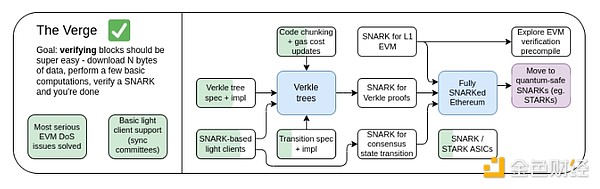
The Verge,2023 年路线圖。
最初,“Verge”指的是將以太坊狀態存儲轉移到 Verkle 樹的想法 - 這種樹結構允許更緊湊的證明,從而實現以太坊區塊的無狀態驗證。節點可以在其硬盤上沒有任何以太坊狀態(账戶余額、合約代碼、存儲……)的情況下驗證以太坊區塊,但代價是花費幾百千字節的證明數據和幾百毫秒的額外時間來驗證證明。如今,Verge 代表了一個更大的愿景,專注於實現以太坊鏈的最大資源效率驗證,其中不僅包括無狀態驗證技術,還包括使用 SNARK 驗證所有以太坊執行。
除了長期關注 SNARK 驗證整個鏈之外,另一個新問題與 Verkle 樹是否是最好的技術有關。 Verkle 樹很容易受到量子計算機的攻擊,因此,如果我們用 Verkle 樹替換當前的 KECCAK Merkle Patricia 樹,我們稍後將不得不再次替換這些樹。 Merkle 樹的自然替代方案是直接跳到在二叉樹中使用 STARK Merkle 分支。從歷史上看,由於开銷和技術復雜性,這被認爲是不可行的。然而,最近,我們看到 Starkware 在帶有 Circle STARK 的筆記本電腦上證明了每秒 170 萬次 Poseidon 哈希值,並且由於 GKR 等技術,更多“傳統”哈希值的證明時間也在迅速縮短。
因此,在過去的一年裏,Verge 變得更加开放,並且存在多種可能性。
The Verge:關鍵目標
無狀態客戶端:完全驗證客戶端和質押節點不需要超過幾 GB 的存儲空間。
(長期)在智能手表上全面驗證鏈(共識和執行)。下載一些數據,驗證 SNARK,完成。
在本文中重點介紹以下內容:
無狀態驗證:Verkle 或 STARKs
EVM執行的有效性證明
共識的有效性證明
無狀態驗證:Verkle 或 STARKs
我們要解決什么問題?
如今,以太坊客戶端需要存儲數百GB的狀態數據才能驗證區塊,並且這個數量每年都在持續增加。原始狀態數據每年增加約 30 GB,個人客戶端除了能夠有效更新 trie 之外還必須存儲一些額外的數據。
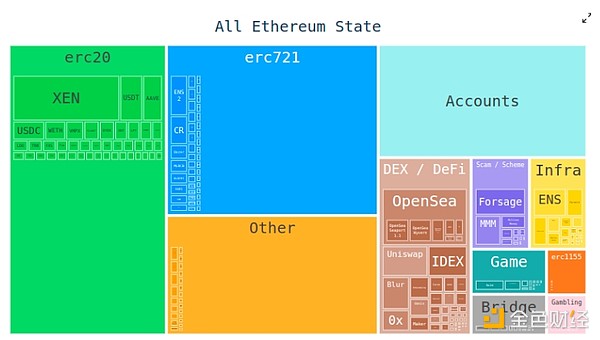
這減少了可以運行完全驗證以太坊節點的用戶數量:盡管硬盤驅動器足夠大,可以存儲所有以太坊狀態甚至多年的歷史記錄,但人們默認購买的計算機往往只有幾百個千兆字節的存儲空間。狀態大小還會給首次設置節點的過程帶來很大的麻煩:節點需要下載整個狀態,這可能需要數小時或數天的時間。這會產生各種連鎖反應。例如,這使得質押者升級其質押設置變得更加困難。從技術上講,可以在不停機的情況下完成此操作 - 啓動新客戶端,等待其同步,然後關閉舊客戶端並傳輸密鑰 —— 但實際上,這在技術上很復雜。
它是什么以及它是如何工作的?
無狀態驗證是一種允許節點在不擁有完整狀態的情況下驗證區塊的技術。相反,每個區塊都帶有一個見證人,其中包括(i)該區塊將訪問的狀態中特定位置的值(例如代碼、余額、存儲),以及(ii)這些值的加密證明是正確的。
實際實現無狀態驗證需要改變以太坊狀態樹結構。這是因爲當前的 Merkle Patricia 樹對於實現任何密碼證明方案都極其不友好,尤其是在最壞的情況下。對於“原始”Merkle 分支以及將 Merkle 分支“包裝”在 STARK 中的可能性都是如此。主要困難源於 MPT 的兩個弱點:
它是一棵六叉樹(即每個節點有 16 個子節點)。這意味着平均而言,大小爲 N 的樹中的證明有 32*(16-1)*log16(N) = 120*log2(N) 字節,或者在 232 項樹中大約有 3840 字節。對於二叉樹,只需要 32*(2-1)*log2(N) = 32*log2(N) 字節,即大約 1024 字節。
該代碼未默克爾化。這意味着提供帳戶代碼的任何訪問權限都需要提供完整的代碼,最大長度爲 24000 字節。
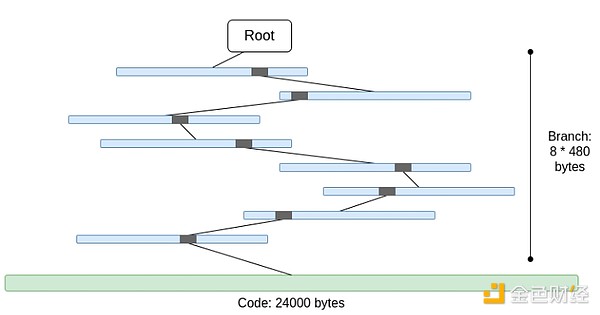
我們可以計算最壞的情況如下:
30,000,000 Gas / 2,400(“冷”账戶讀取成本)* (5 * 480 + 24,000) = 330,000,000 字節
分支成本略有下降(5*480 而不是 8*480),因爲當分支數量很多時,分支的頂部會重復。但即便如此,在一個插槽內下載的數據量也是完全不切實際的。如果我們嘗試將其包裝在 STARK 中,我們會遇到兩個問題:(i) KECCAK 相對 STARK 不友好,(ii) 330 MB 的數據意味着我們必須證明對 KECCAK 輪函數的 500 萬次調用,這是一種方式即使我們可以使 STARK 證明 KECCAK 更加高效,但除了最強大的消費類硬件之外,還有很多東西無法在所有硬件上進行證明。
如果我們只是用二叉樹替換六叉樹,再加上 Merkelize 代碼,那么最壞的情況大約會變成 30,000,000 / 2,400 * 32 * (32 - 14 + 8) = 10,400,000 字節 ~214 個分支,其中 8 是長度進入一片葉子的證明)。請注意,這需要改變Gas成本,以對訪問每個單獨的代碼塊進行收費; EIP-4762 就是這樣做的。 10.4 MB 就好多了,但對於許多節點來說,在一個插槽內下載的數據仍然太多。所以我們需要引入一些更強大的技術。爲此,有兩種主要的解決方案:Verkle 樹和 Starked 二叉哈希樹。
Verkle 樹
Verkle 樹使用基於橢圓曲线的向量承諾來做出更短的證明。關鍵在於,無論樹的寬度如何,每個父子關系對應的證明片段只有 32 個字節。樹寬度的唯一限制是,如果樹太寬,證明的計算效率就會降低。以太坊的建議實現寬度爲 256。
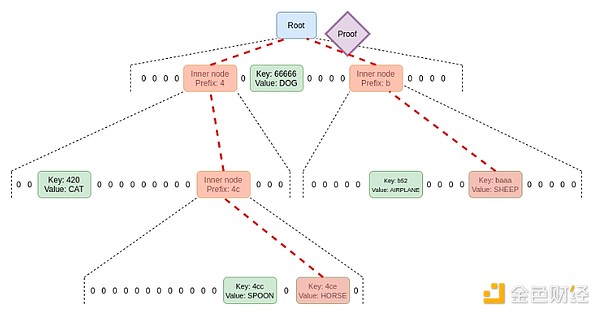
因此,證明中單個分支的大小變爲 32*log256(N) = 4*log2(N) 字節。理論上的最大證明大小變爲大約 30,000,000/2,400*32*(32-14+8)/8 = 1,300,000 字節(由於狀態塊分布不均勻,數學計算在實踐中略有不同,但這作爲第一個很好)。
作爲額外的警告,請注意,在上述所有示例中,這種“最壞情況”並不是最壞情況:更糟糕的情況是攻擊者故意“挖掘”兩個地址以在樹中具有很長的公共前綴,並且從其中一個讀取,這可以將最壞情況的分支長度再延長約 2 倍。但即使有這樣的警告,Verkle 樹也能讓我們獲得約 2.6 MB 的最壞情況證明,這大致與今天的最壞情況呼叫數據相匹配。
我們還利用這個警告來做另一件事:我們使訪問“相鄰”存儲變得非常便宜:同一合約的許多代碼塊,或相鄰的存儲槽。 EIP-4762提供了鄰接的定義,鄰接訪問僅收取200 Gas費用。對於相鄰訪問,最壞情況的證明大小變爲 30,000,000/200*32 = 4,800,800 字節,這仍然大致在容差範圍內。如果爲了安全我們希望降低這個值,我們可以稍微增加相鄰的訪問成本。
已加星標的二元哈希樹
這裏的技術是非常不言自明的:你做一個二叉樹,採用你需要證明一個塊中的值的 max-10.4-MB 證明,並用該證明的 STARK 替換該證明。這讓我們發現證明本身僅包含被證明的數據,加上實際 STARK 的約 100-300 kB 固定开銷。
這裏的主要挑战是證明時間。我們可以進行與上面基本相同的計算,只不過我們不計算字節,而是計算哈希值。 10.4 MB 的塊意味着 330,000 個哈希值。如果我們添加攻擊者“挖掘”樹中具有長公共前綴的地址的可能性,那么真正最壞的情況將變爲大約 660,000 個哈希值。因此,如果我們能夠證明每秒約 200,000 個哈希值,那就沒問題。
這些數字已經在具有 Poseidon 哈希函數的消費筆記本電腦上達到了,該函數是專門爲 STARK 友好性而設計的。然而,波塞冬相對不成熟,因此許多人還不信任它的安全性。因此,有兩條現實的前進道路:
快速對 Poseidon 進行大量安全分析,並熟悉它以將其部署在 L1
使用更“保守”的哈希函數,例如 SHA256 或 BLAKE
在撰寫本文時,Starkware 的 STARK 證明者如果要證明保守的哈希函數,則只能在消費筆記本電腦上每秒證明約 10-30k 哈希值。然而,STARK技術正在迅速進步。即使在今天,基於 GKR 的技術也顯示出有望將其提高到約 100-200k 範圍的潛力。
除了驗證區塊之外的見證人用例
除了驗證塊之外,還有其他三個關鍵用例可以實現更高效的無狀態驗證:
內存池:當交易被廣播時,p2p 網絡中的節點需要在重新廣播之前驗證交易是否有效。如今,驗證不僅包括驗證籤名,還包括檢查余額是否充足以及隨機數是否正確。將來(例如,使用本機帳戶抽象,例如 EIP-7701),這可能涉及運行一些 EVM 代碼,這些代碼會執行一些狀態訪問。如果節點是無狀態的,則交易將需要附帶證明狀態對象的證明。
包含列表:這是一項提議的功能,允許(可能是小型且不復雜的)權益證明驗證器強制下一個塊包含交易,而不管(可能是大型且復雜的)塊構建者的意愿如何。這將降低強大的參與者通過延遲交易來操縱區塊鏈的能力。然而,這要求驗證者有辦法驗證包含列表中交易的有效性。
輕客戶端:如果我們希望用戶通過錢包(例如 Metamask、Rainbow、Rabby...)訪問鏈而不信任中心化參與者,則他們需要運行輕客戶端(例如 Helios)。核心 Helios 模塊爲用戶提供了經過驗證的狀態根。然而,爲了獲得完全去信任的體驗,用戶需要爲他們進行的每個單獨的 RPC 調用提供證明(例如,對於 eth_call 請求,用戶需要在調用期間訪問的所有狀態的證明);
所有這些用例的一個共同點是它們需要相當大量的證明,但每個證明都很小。因此,STARK 證明實際上對他們來說沒有意義;相反,直接使用 Merkle 分支是最現實的。 Merkle 分支的另一個優點是它們是可更新的:給定一個以區塊 B 爲根的狀態對象 X 的證明,如果您收到一個帶有其見證人的子區塊 B2,您可以更新該證明以使其以區塊 B2 爲根。 Verkle 證明本身也是可更新的。
與現有研究有哪些聯系?
Verkle樹:https://vitalik.eth.limo/general/2021/06/18/verkle.html
John Kuszmaul 的原始 Verkle 樹論文:https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf
Starkware 證明數據:https://x.com/StarkWareLtd/status/1807776563188162562
Poseidon2 論文:https://eprint.iacr.org/2023/323
Ajtai(基於格硬度的替代快速哈希函數):https://www.wisdom.weizmann.ac.il/~oded/COL/cfh.pdf
Verkle.info:https://verkle.info/
還需要做什么,需要權衡什么?
剩下要做的主要工作是:
對EIP-4762後果的更多分析(無狀態gas成本變化)
更多工作完成和測試過渡程序,這是任何無狀態 EIP 復雜性的很大一部分
對 Poseidon、Ajtai 和其他“STARK 友好”哈希函數的更多安全分析
進一步开發用於“保守”(或“傳統”)哈希函數的超高效 STARK 協議,例如基於 Binius 或 GKR 的想法。
我們很快就會做出選擇以下三個選項中的哪一個的決策點:(i) Verkle 樹,(ii) STARK 友好的哈希函數,以及 (iii) 保守哈希函數。它們的屬性可以大致總結如下表:
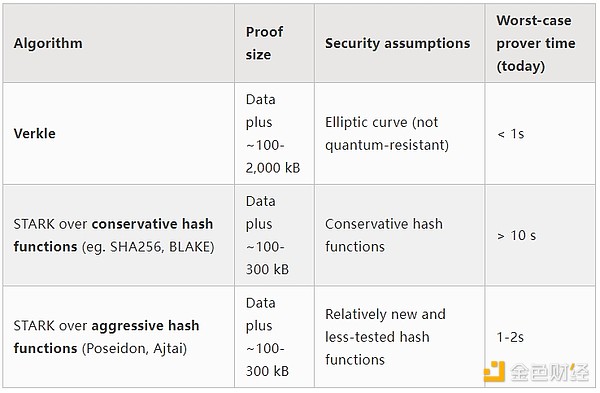
除了這些“標題數字”之外,還有一些其他重要的考慮因素:
如今,Verkle樹代碼已經相當成熟。使用 Verkle 之外的任何東西實際上都會延遲部署,很可能是通過硬分叉。這可能沒問題,特別是如果我們無論如何都需要額外的時間來進行哈希函數分析或證明者實現,並且如果我們有其他重要功能希望盡早包含在以太坊中。
使用哈希更新狀態根比使用 Verkle 樹更快。這意味着基於哈希的方法可以縮短全節點的同步時間。
Verkle 樹具有有趣的見證更新屬性 - Verkle 樹見證是可更新的。此屬性對於內存池、包含列表和其他用例很有用,它還可能有助於提高實現效率:如果更新狀態對象,您可以更新倒數第二個級別的見證人,甚至無需讀取最後一個級別。
Verkle 樹更難通過 SNARK 證明。如果我們想將證明大小一直減少到幾千字節,Verkle 證明會帶來一些困難。這是因爲 Verkle 證明的驗證引入了大量的 256 位操作,這要求證明系統要么具有大量开銷,要么本身具有自定義的內部結構,其中包含用於 Verkle 證明的 256 位部分。
如果我們希望Verkle見證的可更新性以一種量子安全且相當高效的方式進行,另一種可能的途徑是基於網格的Merkle樹。
如果證明系統在最壞的情況下不夠有效,我們可以使用另一個“帽子裏的兔子”來彌補這種不足,那就是多維Gas:對(i) calldata、(ii)計算、(iii)狀態訪問以及可能的其他不同資源有單獨的Gas限制。多維Gas增加了復雜性,但作爲交換,它更嚴格地限制了平均情況和最壞情況之間的比率。對於多維Gas,要證明的理論最大分支數可能會從30,000,000 / 2400 = 12,500減少到3000。 這將使BLAKE3(勉強)即使在今天也足夠了,沒有進一步的證明改進。
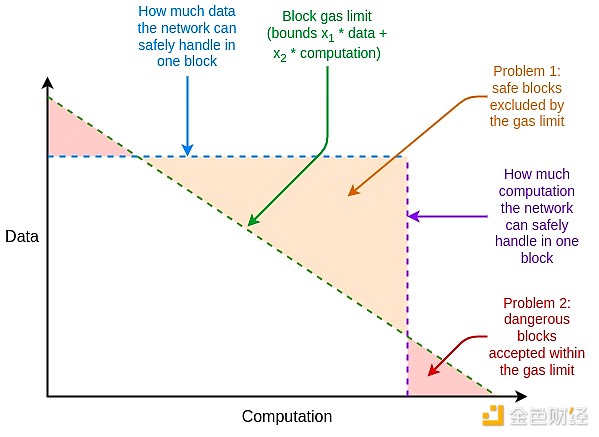
多維Gas允許區塊的資源限制更接近地復制底層硬件的資源限制。
另一個“突然出現的兔子”是延遲狀態根計算直到塊之後的槽的提議。這將爲我們提供整整 12 秒的時間來計算狀態根,這意味着即使在最極端的情況下,只有約 60,000 次哈希/秒的證明時間就足夠了,這再次將我們置於 BLAKE3 勉強夠用的範圍內。
這種方法的缺點是,它會增加輕客戶端延遲一個時間段,盡管該技術有更聰明的版本可以將這種延遲減少到僅證明生成延遲。例如,只要任何節點生成證明,就可以在網絡上廣播該證明,而不是等待下一個塊。
它如何與路线圖的其他部分交互?
解決無狀態問題大大增加了單獨質押的便利性。如果能夠降低單獨質押最低余額的技術(例如 Orbit SSF 或應用層策略(例如小隊質押))變得可用,那么這將變得更有價值。
如果同時引入 EOF,多維Gas會變得更容易。這是因爲用於執行的多維 Gas 的一個關鍵復雜性是處理不傳遞父調用的完整 Gas 的子調用,而 EOF 通過簡單地使此類子調用非法(並且本機帳戶抽象將提供一個 in -當前部分Gas子調用主要用例的協議替代方案)。
另一項重要的協同作用是無狀態驗證和歷史過期之間的協同作用。如今,客戶必須存儲近 TB 的歷史數據;這個數據比國家數據大幾倍。即使客戶端是無國籍的,除非我們也能減輕客戶端存儲歷史的責任,否則客戶端幾乎無存儲的夢想也無法實現。這方面的第一步是 EIP-4444,這也意味着將歷史數據存儲在 torrent 或 Portal 網絡中。
EVM執行的有效性證明
我們要解決什么問題?
以太坊區塊驗證的長期目標很明確:您應該能夠通過以下方式驗證以太坊區塊:(i) 下載該區塊,甚至可能僅下載該區塊的一小部分並進行數據可用性採樣,以及 (ii) 驗證一小部分證明該塊是有效的。這將是一個資源消耗極少的操作,可以在移動客戶端、瀏覽器錢包內甚至(沒有數據可用性部分)在另一個鏈中完成。
要達到這一點,需要擁有 (i) 共識層(即權益證明)和 (ii) 執行層(即 EVM)的 SNARK 或 STARK 證明。前者本身就是一個挑战,應該在進一步改進共識層的過程中解決(例如,單槽最終確定性)。後者需要 EVM 執行的證明。
它是什么以及它是如何工作的?
正式地,在以太坊規範中,EVM 被定義爲狀態轉換函數:你有一些前狀態 S、一個區塊 B,並且你正在計算一個後狀態 S' = STF(S, B)。如果用戶使用的是輕客戶端,他們就沒有S和S',甚至沒有完整的B;相反,它們有一個前狀態根 R、一個後狀態根 R' 和一個塊哈希 H。需要證明的完整語句大約爲:
公共輸入:前狀態根 R、後狀態根 R'、區塊哈希 H。
私有輸入:塊體 B 、塊 Q 訪問的狀態中的對象、執行塊 Q' 後的相同對象、狀態證明(例如 Merkle 分支) P。
主張 1:P 是 Q 包含 R 表示的狀態的某些部分的有效證明。
主張 2:如果您在 Q 上運行 STF,(i) 執行僅訪問 Q 內部的對象,(ii) 該塊有效,並且 (iii) 結果是 Q' 。
主張 3:如果您使用 Q' 和 P 中的信息重新計算新的狀態根,您將得到 R' 。
如果存在,您就可以擁有一個可以完全驗證以太坊 EVM 執行的輕客戶端。這使得客戶端的資源已經相當少了。爲了獲得真正的完全驗證以太坊客戶端,您還需要爲共識方做同樣的事情。
EVM 計算的有效性證明的實現已經存在,並且被L2大量使用。然而,要使 EVM 有效性證明適用於 L1,還有很多工作要做。
與現有研究有哪些聯系?
EC PSE ZK-EVM(現已廢棄,因爲存在更好的選擇):https://github.com/privacy-scaling-explorations/zkevm- Circuits
Zeth,其工作原理是將 EVM 編譯到 RISC-0 ZK-VM 中:https://github.com/risc0/zeth
ZK-EVM形式化驗證項目:https://verified-zkevm.org/
還需要做什么,需要權衡什么?
如今,EVM 的有效性證明在兩個方面都不夠充分:安全性和證明時間。
安全有效性證明需要確保 SNARK 確實驗證了 EVM 計算,並且其中沒有錯誤。提高安全性的兩種主要技術是多重證明者和形式驗證。多證明者意味着擁有多個獨立編寫的有效性證明實現,就像有多個客戶端一樣,並且如果這些實現的足夠大的子集證明了某個塊,則讓客戶端接受該塊。形式驗證涉及使用常用於證明數學定理的工具(例如 Lean4)來證明有效性證明僅接受以 Python 編寫的底層 EVM 規範的正確執行的輸入。
足夠快的證明時間意味着任何以太坊區塊都可以在不到 4 秒的時間內得到證明。今天,我們距離這個目標仍然很遠,盡管我們比兩年前的想象要近得多。爲了實現這一目標,我們需要在三個方面推進:
並行化——當今最快的 EVM 證明者可以在約 15 秒內證明平均以太坊區塊。它通過在數百個 GPU 之間進行並行化,然後最後將它們的工作聚合在一起來實現這一點。理論上,我們確切地知道如何制作一個可以在 O(log(N)) 時間內證明計算的 EVM 證明器:讓一個 GPU 執行每個步驟,然後執行“聚合樹”:
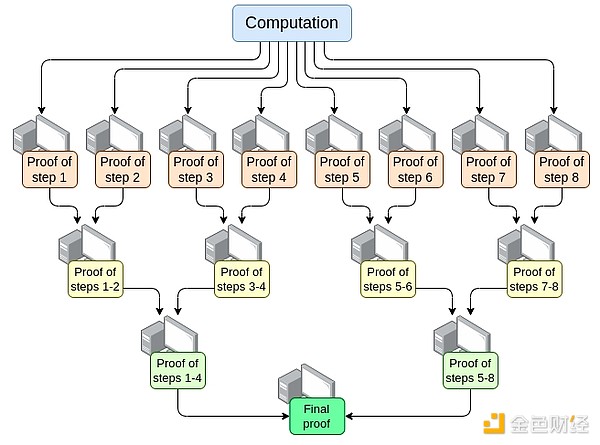
實施這一點存在挑战。即使在最壞的情況下(即非常大的交易佔用整個塊)也能工作,計算的分割不能是按交易進行的;它必須是每個操作碼(EVM 或底層 VM(如 RISC-V))。使這變得不完全微不足道的一個關鍵實現挑战是需要確保VM的“內存”在證明的不同部分之間是一致的。然而,如果我們可以進行這種遞歸證明,那么我們知道至少證明者延遲問題得到了解決,即使在任何其他軸上沒有任何改進。
證明系統優化 —— Orion、Binius、GKR 等新的證明系統可能會導致通用計算的證明時間再次大幅減少。
EVM 的 Gas 消耗了其他變化 —— EVM 中的許多東西都可以優化,使其對證明者更加友好,尤其是在最壞的情況下。如果攻擊者能夠構建一個會佔用證明者十分鐘時間的區塊,那么僅僅在 4 秒內證明一個平均以太坊區塊是不夠的。所需的 EVM 更改主要可以分爲兩類:
Gas 成本變化 —— 如果一個操作需要很長時間來證明,那么即使計算速度相對較快,它也應該具有較高的 Gas 成本。 EIP-7667 是一個提議的 EIP,用於處理這方面最嚴重的問題:它顯著增加了作爲相對便宜的操作碼和預編譯公开的(傳統)哈希函數的 Gas 成本。爲了補償這些 Gas 成本的增加,我們可以降低證明相對便宜的 EVM 操作碼的 Gas 成本,從而保持平均吞吐量相同。
數據結構替換 —— 除了用更適合 STARK 的替代方案替換狀態樹之外,我們還需要替換交易列表、收據樹和其他證明成本高昂的結構。 Ethan Kissling 的 EIP 將交易和收據結構移至 SSZ ([1] [2] [3]),這是朝這個方向邁出的一步。
除此之外,上一節中提到的兩個“從帽子裏出來的兔子”(多維Gas和延遲狀態根)也可以在這裏提供幫助。然而,值得注意的是,與無狀態驗證不同,無狀態驗證意味着我們有足夠的技術來完成我們今天所需要的事情,即使使用這些技術,完整的 ZK-EVM 驗證也將需要更多的工作 —— 只是需要更少的工作工作。
上面沒有提到的一件事是證明硬件:使用 GPU、FPGA 和 ASIC 更快地生成證明。 Fabric Cryptography、Cysic 和 Accseal 是這三家公司的推動者。這對於第 2 層來說非常有價值,但它不太可能成爲第 1 層的決定性考慮因素,因爲人們強烈希望保持第 1 層高度去中心化,這意味着證明生成必須在相當大的子集的能力範圍內。以太坊用戶,不應該遇到單一公司硬件的瓶頸。第 2 層可以做出更激進的權衡。
這些領域還有更多工作要做:
並行證明需要證明系統,其中證明的不同部分可以“共享內存”(例如查找表)。我們知道做到這一點的技術,但它們需要實施。
我們需要更多的分析來找出理想的 Gas 成本變化集,以最大限度地減少最壞情況下的證明時間。
我們需要在證明系統上做更多的工作
這裏可能的權衡包括:
安全性與證明者時間:使用哈希函數的積極選擇、具有更復雜性或更積極的安全假設的證明系統或其他設計選擇,可能會減少證明者時間。
去中心化與證明者時間:社區需要就其目標證明者硬件的“規範”達成一致。要求證明者是大規模實體可以嗎?我們是否希望高端消費筆記本電腦能夠在 4 秒內證明以太坊區塊?介於兩者之間的東西嗎?
破壞向後兼容性的程度:其他領域的不足可以通過進行更積極的 Gas 成本更改來彌補,但這更有可能不成比例地增加某些應用程序的成本,並迫使开發人員重寫和重新部署代碼,以便保持經濟可行性。同樣,“帽子裏的兔子”也有其自身的復雜性和缺點。
它如何與路线圖的其他部分交互?
在第 1 層實現 EVM 有效性證明所需的核心技術與其他兩個領域大量共享:
第 2 層的有效性證明(即“ZK rollups”)
“STARK 二進制哈希證明”無狀態方法
在第 1 層成功實施有效性證明可以實現最終的輕松單獨質押:即使是最弱的計算機(包括手機或智能手表)也能夠進行質押。這進一步增加了解決單獨質押其他限制的價值(例如最低 32 ETH)。
此外,L1 的 EVM 有效性證明可以顯著提高 L1 的 Gas 限制。
共識的有效性證明
我們要解決什么問題?
如果我們希望能夠用 SNARK 完全驗證以太坊區塊,那么 EVM 執行並不是我們需要證明的唯一部分。我們還需要證明共識:系統中處理存款、取款、籤名、驗證者余額更新以及以太坊權益證明部分的其他元素的部分。
共識比 EVM 簡單得多,但它面臨的挑战是我們沒有第 2 層 EVM 匯總,這也是大多數工作無論如何都要完成的原因。因此,任何證明以太坊共識的實現都需要“從頭开始”完成,盡管證明系統本身是可以構建在其之上的共享工作。
它是什么以及它是如何工作的?
信標鏈被定義爲狀態轉換函數,就像 EVM 一樣。狀態轉移函數由三個因素決定:
ECADD(用於驗證 BLS 籤名)
配對(用於驗證 BLS 籤名)
SHA256 哈希(用於讀取和更新狀態)
在每個區塊中,我們需要爲每個驗證器證明 1-16 個 BLS12-381 ECADD(可能不止一個,因爲籤名可以包含在多個聚合中)。這可以通過子集預計算技術來補償,因此我們可以說每個驗證器都是一個 BLS12-381 ECADD。如今,每個時段都有約 30,000 名驗證者籤名。將來,對於單時隙最終確定性,這可能會向任一方向發生變化(請參閱此處的說明):如果我們採取“強力”路线,則每個時隙可能會增加到 100 萬個驗證器。同時,使用 Orbit SSF,它將保持在 32,768,甚至減少到 8,1。
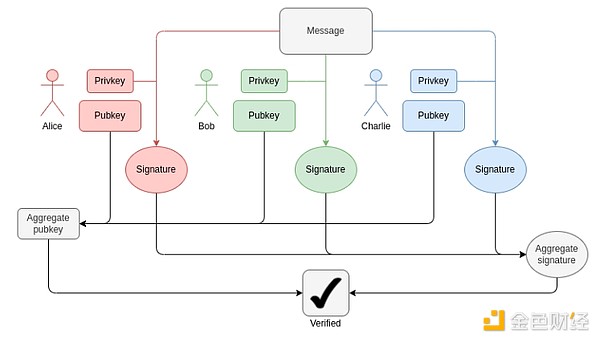
BLS 聚合的工作原理。驗證聚合籤名僅需要每個參與者的 ECADD,而不是 ECMUL。但 30,000 個 ECADD 仍然有很多需要證明的地方。
對於配對,當前每個插槽最多有 128 個證明,這意味着需要驗證 128 個配對。通過 EIP-7549 和進一步的更改,這可能會減少到每個插槽 16 個。配對數量很少,但成本極高:每一對的運行(或證明)時間比 ECADD 長數千倍。
證明 BLS12-381 操作的一個主要挑战是沒有方便的曲线,其曲线階數等於 BLS12-381 字段大小,這給任何證明系統增加了相當大的开銷。另一方面,爲以太坊提出的 Verkle 樹是用 Bandersnatch 曲线構建的,這使得 BLS12-381 本身成爲 SNARK 系統中用來證明 Verkle 分支的自然曲线。一個相當簡單的實現每秒可以提供約 100 個 G1 添加;幾乎肯定需要像 GKR 這樣的聰明技術才能足夠快地證明。
對於 SHA256 哈希值,目前最糟糕的情況是紀元轉換塊,其中整個驗證器短平衡樹和大量驗證器余額都會更新。驗證器短平衡樹每個驗證器只有一個字節,因此約 1 MB 的數據會被重新散列。這相當於 32,768 次 SHA256 調用。如果一千個驗證者的余額高於或低於閾值,則需要更新驗證者記錄中的有效余額,這對應於一千個 Merkle 分支,因此可能還有一萬個哈希值。混洗機制需要每個驗證器 90 位(因此需要 11 MB 數據),但這可以在一個 epoch 過程中的任何時間進行計算。對於單時隙最終性,這些數字可能會根據細節再次增加或減少。洗牌變得不必要,盡管軌道可能會在某種程度上恢復對洗牌的需要。
另一個挑战是需要讀取所有驗證器狀態(包括公鑰)才能驗證塊。對於 100 萬個驗證器,加上 Merkle 分支,僅讀取公鑰就需要 4800 萬字節。這需要每個時期數百萬個哈希值。如果我們今天必須證明權益證明驗證,那么一種現實的方法是某種形式的增量可驗證計算:在證明系統中存儲一個單獨的數據結構,該數據結構針對高效查找進行了優化,並提供對此結構的更新。
總而言之,存在很多挑战。
要最有效地解決這些挑战很可能需要對信標鏈進行深入的重新設計,這可能與切換到單時隙最終性同時發生。此次重新設計的特點可能包括:
哈希函數更改:今天,使用“完整”SHA256 哈希函數,因此由於填充,每個調用對應於兩個底層壓縮函數調用。至少,我們可以通過切換到 SHA256 壓縮功能來獲得 2 倍的增益。如果我們改用 Poseidon,我們可以獲得大約 100 倍的增益,這可以完全解決我們所有的問題(至少對於哈希):每秒 170 萬個哈希(54 MB),甚至可以“讀取一百萬個驗證器記錄” ” “幾秒鐘內就可以證明。
如果是 Orbit,則直接存儲打亂的驗證者記錄:如果您選擇一定數量的驗證者(例如 8,192 或 32,768)作爲給定槽的委員會,則將它們直接放入彼此相鄰的狀態,以便最小哈希量爲需要將所有驗證器公鑰讀入證明中。這也將使所有余額更新能夠有效地完成。
籤名聚合:任何高性能籤名聚合方案實際上都會涉及某種遞歸證明,其中籤名子集的中間證明將由網絡中的各個節點進行。這自然地將證明負載分散到網絡中的許多節點上,從而使“最終證明者”的工作量小得多。
其他籤名方案:對於Lamport+Merkle籤名,我們需要256+32個哈希來驗證籤名;乘以 32,768 個籤名者得到 9,437,184 個哈希值。對籤名方案的優化可以通過一個小的常數因子進一步改善這一點。如果我們使用波塞冬,這在單個槽內證明的範圍內。但實際上,通過遞歸聚合方案,這會變得更快。
與現有研究有哪些聯系?
簡潔,以太坊共識證明(僅限同步委員會):https://github.com/succinctlabs/eth-proof-of-consensus
簡潔,SP1 內的 Helios:https://github.com/succinctlabs/sp1-helios
簡潔的 BLS12-381 預編譯:https://blog.succinct.xyz/succinctshipsprecompiles/
基於 Halo2 的 BLS 聚合籤名驗證:https://ethresear.ch/t/zkpos-with-halo2-pairing-for-verifying-aggregate-bls-signatures/14671
還需要做什么,需要權衡什么?
實際上,我們需要數年時間才能得到以太坊共識的有效性證明。這與我們需要實現單槽最終性、軌道、籤名算法的更改以及潛在的安全分析所需的時間线大致相同,以便有足夠的信心使用像 Poseidon 這樣的“激進”哈希函數。因此,解決這些其他問題是最有意義的,並且在做這些工作時要牢記 STARK 友好性。
主要的權衡很可能是在操作順序上,在改革以太坊共識層的更漸進的方法和更激進的“一次進行許多改變”的方法之間。對於 EVM,增量方法很有意義,因爲它可以最大限度地減少對向後兼容性的破壞。對於共識層來說,向後兼容性問題較小,並且更“全面”地重新思考信標鏈如何構建的各種細節,以最好地優化 SNARK 友好性是有好處的。
它如何與路线圖的其他部分交互?
STARK 友好性需要成爲以太坊權益證明共識的長期重新設計的主要關注點,最顯著的是單槽最終性、Orbit、籤名方案的更改和籤名聚合。
鄭重聲明:本文版權歸原作者所有,轉載文章僅為傳播信息之目的,不構成任何投資建議,如有侵權行為,請第一時間聯絡我們修改或刪除,多謝。
