格密碼的量子危機?一文帶你解析格密碼學術風波

 ZAN Team
個人專欄
剛剛
ZAN Team
個人專欄
剛剛
區塊鏈的量子安全威脅以及應對
2024 年 3 月 10 日,以太坊聯合創始人 Vitalik Buterin 在以太坊研究論壇(ethresear.ch)發布最新文章《How to hard-fork to save most user's funds in a quantum emergency》[1],文中表示:以太坊生態系統面臨的量子計算攻擊威脅,可以通過恢復性分叉策略和抗量子密碼技術來保護用戶資金安全。
對於區塊鏈來說,量子安全威脅到底是什么?
量子計算 [2] 作爲利用量子力學調控量子信息單元進行計算的新型計算模式,在 20 世紀 80 年代被提出,在其概念提出後的十年內,量子計算機也只是停留在抽象理論階段。直到 20 世紀 90 年代中期的兩個量子算法:Shor 算法 [3](多項式時間內解決大數分解及離散對數困難問題)和Grover算法 [4](針對非結構化數據的窮舉搜索問題提供平方加速)的提出,使得量子計算跳出抽象理論階段,轉而進入到物理載體研發的新階段,也就是目前所說的量子計算機。下圖展示了從 1998 年到 2026 年量子計算機的物理量子比特發展路线圖:
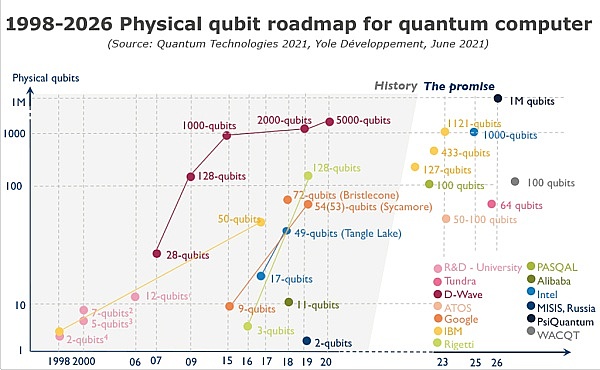
量子計算不是萬能的,它並非能解決所有計算問題。目前可在模擬(模擬自然界發生的過程,適用於化學與生物工程)、破譯(打破大部分傳統密碼體系,適用於網絡安全)、優化(尋找可行選項中的最優解,適用於金融、供應鏈)等特定領域問題上發揮其計算優越性。
區塊鏈目前得到廣泛應用來自於它給不同訴求方間的協作帶來新的信任基礎,而這種信任基礎建立在底層密碼學所提供的安全性保障之上:
信身份與交易確權:基於非對稱公私鑰對建立用戶可信身份,統一管理身份信息。通過數字籤名實現數字資產的確權,有效籤名的私鑰持有者實際擁有資產所有權。
核心共識和運行安全:基於哈希函數、門限籤名、可驗證隨機函數等現代密碼技術構建共識機制,保障共識機制使用安全。
隱私保護與安全共享:基於零知識證明、安全多方計算、全同態等富功能密碼技術構建隱私保護方案,實現區塊鏈上數據的安全共享。
可控監管與合規應用:集成部署環籤名、同態密碼方案、隱地址和祕密共享等密碼技術,確保區塊鏈交易的安全監管。
這其中涉及到公鑰密碼的用法可粗略分爲:鏈上交易防篡改使用的數字籤名機制,以及節點間通信使用的安全傳輸協議。受 Shor 算法的影響,上述公鑰密碼在使用上的安全性無法得到有效保障。在考慮專用密碼破譯量子計算機大規模應用所需時間的同時,還需考慮存儲在區塊鏈上的數據需要保存多長時間以及現有區塊鏈系統升級到量子安全級別的時間。如果後兩者相加的時間和大於前者,那么區塊鏈上的數據就會受到量子計算帶來的嚴重安全威脅。
考慮到量子計算飛速發展帶來的算力不斷提升的現狀,目前可以有效應對安全風險的主要有兩種技術途徑:
不借助物理設備的基於新型數學難題的後量子密碼 [5] 技術路线;
借助專用物理設備的基於物理原理的量子密碼 [6] 技術路线。
綜合考慮落地實施驗證等多種因素,爲確保區塊鏈長期演進下的安全性保證,在兼容現有密碼安全的前提下,可考慮通過後量子密碼遷移將區塊鏈提前部署升級到量子安全級別。理想情況下,將現有區塊鏈使用的公鑰密碼算法升級爲量子安全的後量子密碼算法,應盡可能滿足以下特點:
密鑰小且籤名短:區塊鏈上的每筆交易都會包含籤名信息,而驗證任意一筆交易的公鑰也存儲在鏈上。若密鑰以及籤名尺寸過大,都將大大加劇區塊鏈的存儲成本以及通信开銷;
計算效率高:區塊鏈運行時每一時間段可處理的交易數量很大程度上與算法的運行時間有關,特別是籤名驗籤算法。算法更快的計算效率可以更好地支持高性能的區塊鏈應用。
後量子密碼發展現狀
後量子密碼,一句話概括就是能夠抵抗量子計算機對現有密碼算法攻擊的第一代密碼算法:
面向公鑰密碼體系;
依賴新型數學問題;
不需要專用設備支持;
經典計算以及量子計算條件下安全;
目前主流的構造技術路线有五種,如下圖所示,從左到右分別是格、編碼、多變量、哈希以及同源:
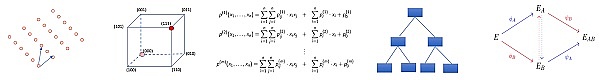
格:基於格上的困難問題。
編碼:基於解碼的困難性。
多變量:基於有限域上多元二次多項式組的難解性。
哈希:基於哈希函數的抗碰撞性。
同源:基於超奇異橢圓曲线的僞隨機遊走。
新一代密碼算法然會涉及到標准密碼體系的建立。關於後量子密碼標准最值得關注的則是:美國國家標准技術研究所(NTST)的後量子密碼標准化項目 [7],從 2016 年啓動到現在已基本進入後量子密碼標准化制定的尾聲。回顧這接近十年的標准化時間线,NIST 在:
2022 年 7 月 5 日,正式官宣四個後量子密碼標准候選算法 [8]:
公鑰加密/密鑰封裝:CRYSTALS-KYBER;
數字籤名:CRYSTALS-Dilithium、FALCON;SPHINCS+;
這其中,CRYSTALS-KYBER、CRYSTALS-Dilithium、FALCON 均爲格密碼算法,但三者的安全性基礎有所區別,KYBER 基於模格的 MLWE 困難問題,Dilithium 基於模格的 MLWE 和 MSIS 困難問題,FALCON 則基於 NTRU 格的 SIS 困難問題;除此之外,SPHINCS+ 是無狀態哈希籤名算法。
2023 年 8 月 24 日,已將 CRYSTALS-KYBER、CRYSTALS-Dilithium、SPHINCS+分別形成FIPS203、FIPS 204、FIPS205 標准草案 [9],FALCON 標准草案也將在 2024 年公布。
不難看出目前 NIST 選擇的標准算法大多基於格密碼的技術路线。但是 NIST 並沒有把雞蛋放在同一個籃子中,他們也在積極需要除了格構造以外的多種選擇:2022 年公布四個標准算法的同時,也宣布啓動了第四輪後量子密碼標准算評估工作,這一輪則關注於公鑰加密/密鑰封裝算法,入選的算法並沒有基於格構造。此外,還發起新一輪數字籤名算法的徵集,此輪徵集獨立於第四輪評估獨立進行,旨在豐富後量子籤名算法組合,所以更關注於算法構造上不同與現有的基於結構格,且算法籤名尺寸小、驗證速度快的新提案。
除了 NIST 標准外,國際互聯網標准化組織 IETF 在 2018 年和 2019 年分別標准化有狀態哈希籤名算法 XMSS 爲 RFC 8391[10]、LMS 爲 RFC 8554[11] 且被 NIST 接受。
破解格密碼的量子算法
2024 年 4 月 10 日,陳一鐳老師在 eprint 上的文章《Quantum Algorithms for Lattice Problems》[12] 引起了學術界的轟動。論文中給出了一種多項式時間求解格上困難問題的量子算法,該算法對很多基於格困難問題的密碼方案有着較大衝擊,可導致很多算法不再具備抗量子計算機攻擊的能力,例如,目前廣泛使用的基於 LWE 假設的同態加密算法。論文中算法的正確性暫未可知。
LWE 問題的困難性由 Oded Regev 在論文《On lattices, learning with errors, random linear codes, and cryptography》[13] 中給出了嚴格的論證,具體地說,作者在論文中將 LWE 問題的困難性歸約到格上的離散高斯採樣問題,而離散高斯採樣問題可以很容易歸約到 GapSVP, SIVP 等經典問題(當然,每個具體問題都是有其具體參數的,這裏忽略),這說明 LWE 問題要比這些經典的格問題還要困難。在 LWE 問題的困難性有了嚴格的歸約後,由於其結構簡單,一大批基於 LWE 的密碼方案也隨之而來,涵蓋(同態)加密,籤名,密鑰交換等基礎密碼原語,以及基於身份加密,屬性加密等高級密碼原語等。其中,在業界使用較多的主要集中在全同態加密和上面所提到的 NIST 公布的後量子標准算法(KYBER, Dilithium等)。


總結
該論文公开後,對學術界造成了很大的轟動,引起很多專業人士的討論。但由於論文的理解難度極大,全世界可能也就不到 5 位學者可以完全理解論文的內容,可能需要 1-2 年的時間才能完全驗證論文的正確性。目前一些論壇、公衆號、知乎等平台也有很多人發表了一些相關見解,大家都是在分析如果論文中的算法是正確的,會帶來哪些影響,至於論文算法的正確性問題,還沒人能下定結論。其中,著名密碼學家 N. P. Smart 發表了博客文章《Implications of the Proposed Quantum Attack on LWE》[14],詳細介紹了此攻擊的影響和一些觀點,總結如下:
這篇論文目前尚未經過同行評審,即使被驗證是正確的,也要依賴於量子計算機,因此只要量子計算機還未問世,對目前在使用的密碼方案均無影響。
按照論文中給出的結果:仍無法攻破此前 NIST 給出的標准化算法 Kyber, Dilithium,但 NIST 可能會重新評估這些算法的參數。
對於常用的 RLWE 同態加密算法,如 BFV/CKKS/BGV,這些算法是在這篇論文的攻擊能力之內的。不過,不管從是學術界還是工業界的視角,同態加密技術的“同態性”比其“抗量子性”更具吸引力,很少人會爲追求“抗量子性”而使用 RLWE 同態加密算法,就像基於橢圓曲线的密碼方案依賴於離散對數困難問題,而求解該問題的量子算法很早就被提出了,但學術界,工業界仍然在研究、使用這些方案。
最新消息:陳老師論文計算存在問題,格密碼警報暫時解除。

[1] https://ethresear.ch/t/how-to-hard-fork-to-save-most-users-funds-in-a-quantum-emergency/18901/9
[2] Benioff P. The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines[J]. Journal of statistical physics, 1980, 22: 563-591.
[3] Shor P W. Algorithms for quantum computation: discrete logarithms and factoring[C]//Proceedings 35th annual symposium on foundations of computer science. Ieee, 1994: 124-134.
[4] Grover L K. A fast quantum mechanical algorithm for database search[C]//Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. 1996: 212-219.
[5] Bernstein, D.J. (2009). Introduction to post-quantum cryptography. In: Bernstein, D.J., Buchmann, J., Dahmen, E. (eds) Post-Quantum Cryptography. Springer, Berlin, Heidelberg.
[6] Gisin N, Ribordy G, Tittel W, et al. Quantum cryptography[J]. Reviews of modern physics, 2002, 74(1): 145.
[7] https://csrc.nist.gov/Projects/post-quantum-cryptography/post-quantum-cryptography-standardization
[8] https://csrc.nist.gov/News/2022/pqc-candidates-to-be-standardized-and-round-4
[9] https://csrc.nist.gov/News/2023/three-draft-fips-for-post-quantum-cryptography
[10] Huelsing, A., Butin, D., Gazdag, S., Rijneveld, J., and A. Mohaisen, "XMSS: eXtended Merkle Signature Scheme", RFC 8391, DOI 10.17487/RFC8391, May 2018, <https://www.rfc-editor.org/info/rfc8391>.
[11] McGrew, D., Curcio, M., and S. Fluhrer, "Leighton-Micali Hash-Based Signatures", RFC 8554, DOI 10.17487/RFC8554, April 2019, <https://www.rfc-editor.org/info/rfc8554>.
[12] Chen Y. Quantum Algorithms for Lattice Problems[J]. Cryptology ePrint Archive, 2024.
[13] Regev O. On lattices, learning with errors, random linear codes, and cryptography[J]. Journal of the ACM (JACM), 2009, 56(6): 1-40.
[14] https://nigelsmart.github.io/LWE.html
本文由 ZAN Team(X 账號 @zan_team)的 Dongni 和 Jiaxing 共同撰寫。
鄭重聲明:本文版權歸原作者所有,轉載文章僅為傳播信息之目的,不構成任何投資建議,如有侵權行為,請第一時間聯絡我們修改或刪除,多謝。
