作者：Arweave Oasis，來源：PermaDAO

本文有些硬核，因爲會有很多數學推導論證過程，各位朋友要作好准備。但筆者認爲數學作爲基礎學科，在從邏輯上解釋一個事物有着極強的精准性，所以不妨讓筆者試試用簡單的語言來展示 @ArweaveEco 機制中的數學之美。

在白皮書解讀（二）文章中，我們描述了簡潔訪問證明（ #SPoA ）遊戲可以被任何參與者用來證明他們在數據集的特定位置確實存儲了一些數據。這個模式還可以用來創建第二個遊戲，我們稱其爲簡潔的復制證明（Succinct Proofs of Replications #SPoRes ），這將允許證明者無論數據集大小如何，都能以極小的數據傳輸和驗證成本，來向驗證者證明自己存儲了一定數量的數據副本。

SPoRes 遊戲

簡潔的復制證明（SPoRes）遊戲是這樣進行的。Alice 聲稱她存儲了 n 份默克爾化數據集的唯一副本。Bob 想要驗證 Alice 有沒有說謊。爲了做到這一點，他給 Alice 一個難度參數 d 和一個隨機產生的種子 Seed。Alice 使用這個 Seed 生成一個每秒鐘發出一個檢查點的 VDF 哈希鏈，這個檢查點可以用來解鎖數據集內最多 k 個 SPoA 挑战。每當她有對應於這些挑战的打包數據塊時，Alice 可以構建相應的 SPoA 證明。然後將這些證明進行哈希處理，並與 Bob 的難度參數 d 進行對比。如果證明哈希值大於 d，則 Alice 找到了一個有效解決方案，並將相應的證明發送給 Bob。Bob 則記錄下發送隨機種子到收到 Alice 有效證明之間的時間。

基於難度 d，單次嘗試找到有效解決方案的概率 p 的表達式爲：

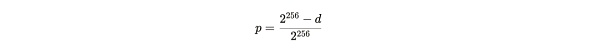
公式注解：由於基於 SHA 256 的算法是一個 256 位字符串，所以就有 2^256 (這裏「^」表示的是次方的意思) 個最大哈希數量，如果要找到大於 d 的有效解決方案，那只有 2^256-d 個哈希數量，以此可以計算出單次嘗試成功的概率。

如果 Alice 有 n 個副本，並且每秒每個副本可以進行 k 次嘗試，那么她在任何給定的一秒時間內找到解決方案的概率是：

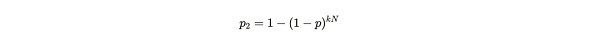
公式注解：kN 的意思爲 Alice 在一秒內總共可以進行的哈希解決方案嘗試次數，這個嘗試次數與 Alice 存儲的唯一副本數量成正比，具體解釋可以閱讀此前文章 《Arweave 2.6 也許更符合中本聰的愿景》的內容。1-p 是單次嘗試失敗的概率。p2 的概率值就是 1 減去 kN 次嘗試失敗的概率的差。

通過上述兩個公式的代入推導，我們可以得到：

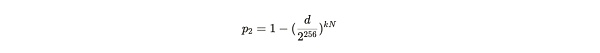
公式注解：將 p 代入至 P2 的公式中所得結果

Alice 提交證明所需的時間可以用一個幾何隨機變量 X ~ geom(p2) 來模擬，p2 爲成功的概率。這個隨機變量 X 取決於 d，k 和 n。爲了驗證 Alice 是否說謊，Bob 發送一個難度 d，使 Alice 以有 n 個副本的前提下，可以每 120 秒向 Bob 提交一次證明。這相當於 Alice 在 120 秒的成功概率爲：

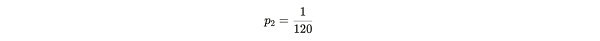
公式注解：1/120 爲 120 秒內成功提交一次證明的概率

如果 Alice 可以在要求的時間內提交證明，那她很可能擁有正確數量的唯一副本。但一次證明是不足以讓 Bob 確信 Alice 沒有說謊，如果 Alice 能在很長一段時間內平均每 120 秒一直提交證明，Bob 才可以合理地確信 Alice 存儲了符合期望的數據量。

接下來我們嘗試去量化 Bob 對 Alice 存儲的確定性。

假設 Alice 聲稱存儲了 20 個副本，並且在 2 周的時間內以平均 120 秒的速度一致地提交了證明（總共提交了 10,080 個證明）。此時，Bob 在想如果 Alice 只存儲了 19 個（或更少）的副本，她依然能提交這些證明的概率是多少。這對應於在不同的一秒鐘內提供證明的概率：

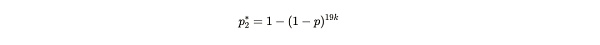
公式注解：這裏出現的 19k，就是 Alice 存了 19 個副本，每個副本擁有 k 次嘗試尋找解決方案的次數。

過簡化:

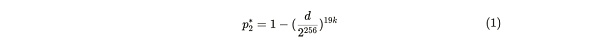
這個概率可以使用 Bob 爲誠實的 Alice 生成的 d 值來計算。如果她存儲了 19 個或更少的副本，她一秒鐘內提供證明的概率可以通過下面給出的一系列推導得到。其中， p2 代表了 Alice 誠實存儲了 20 個副本時，一秒內生成證明的概率，而 p2* 則代表如果她在說謊（存儲≤ 19 個副本）時，一秒內提供證明的概率：

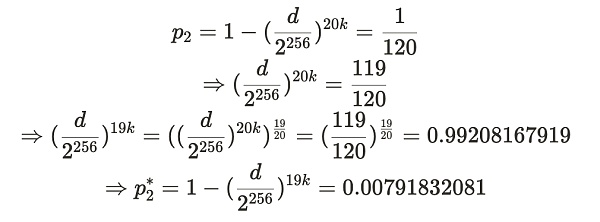
這個推導過程看似很復雜，其實有基礎數學能力的朋友就都能看懂。推導過程就是上述公司的代入過程。

因此，p2*=0.00791832081，對應於預期的證明生成時間爲 126.2894 秒。設 X* 爲從 p2* 得到的 Alice 提交證明的時間，即 X*~ geom(p2*) 。這代表了 Alice 在說謊情況下 —— 只存儲了 19 個副本，所花去的提交證明的時間 X* 的期望值（平均值）是：

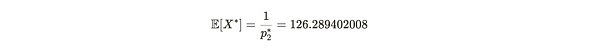
公式注解：E[X*] 表示 Alice 在只存儲了 19 個副本的前提下，成功提交證明的平均時間在 126.2894 秒。而如果她存儲了 20 個副本，成功提交時間則平均在 120 秒。

我們可以使用中心極限定理來估算樣本均值低於 120 的概率，即與上述得到的期望值 E[X*] 不同。這個概率表示爲：

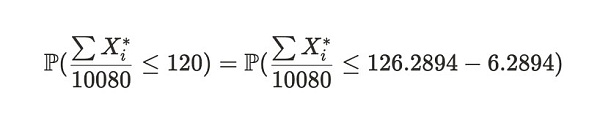
公式注解：等式左邊表達式代表在兩周時間內，Alice 平均每次提交證明的時間小於等於 120 秒的概率。等式右邊則是左邊表達式的變體。

對於大量樣本來說，這個不等式左側趨向於一個均值爲 E[X*] 和方差爲 σX*^2/n的正態分布，其中 σX* 是 Xd 的標准差，n (這裏 =10,080)是樣本大小。因此，上述公式可以變爲：

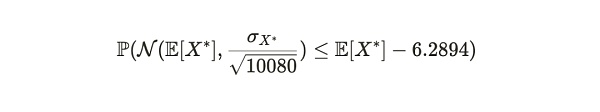
我們可以將這個分布轉換爲標准正態形式，以獲得等價的概率：

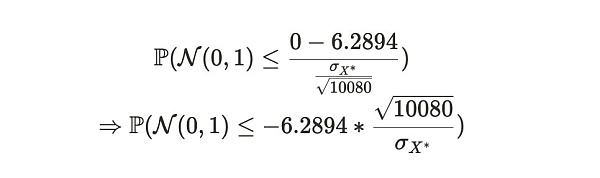
最終，使用標准正態分布表，我們可以獲得 Alice 在這周時間周期中說謊的概率：

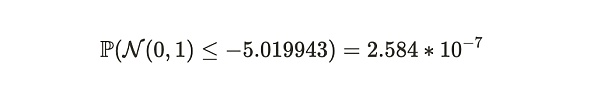
因此，在這個例子中，Bob 可以以約 99.99997416% 的確定性判斷，在這 2 周時間裏 Alice 存儲了超過 19 份數據集的副本。我們注意到，如果 Alice 存儲的副本少於 19 份，預期的證明提交時間將大於 126.3 秒。我們還注意到，整個證明系統僅需要每 120 秒傳輸一次證明。這是 Alice 和 Bob 之間的平均數據傳輸率爲每秒 2.389 KB（280 KB/120 秒），與比特幣網絡的同步开銷相當。

最後，這些概率不會隨着數據集大小的任意增加而改變，而增加採樣周期將以超线性的速率持續提高 Bob 對 Alice 副本數量的確定性的准確度（圖1）。

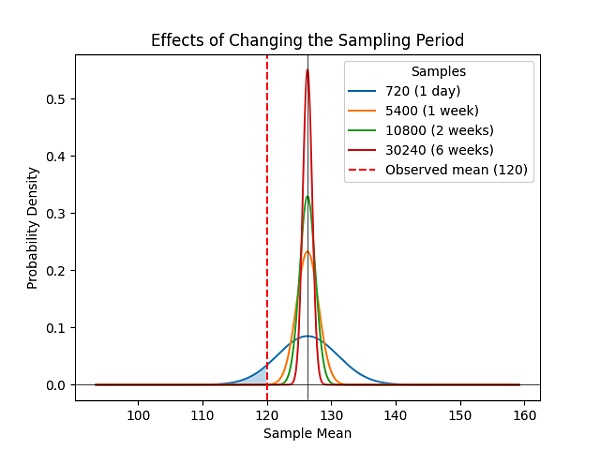
圖 1：在簡潔復制證明（SPoRes）遊戲中，確定性相對於樣本持續時間的增加是超线性的。經過兩周的樣本收集，維持少於 19 個副本的概率是微不足道的（P<0.0000002584）。

所以，一個 SPoRes 遊戲由以下參數定義：

其中：

r= 用於遊戲的數據集的默克爾根。

k= 每個副本每秒鐘解鎖的最大的挑战數量。

d= 決定每次嘗試時的成功概率的難度參數。

通過這些有趣的數學推導，我們可以放心地確定，只要在一個合理的時間段中讓礦工持續提交證明就能確定數據是否被儲存。這構成了 Arweave 以去中心化存儲爲目標的共識機制的核心。數學的樂趣才剛剛开始，接下來的文章中還會有更多有趣的推演與論證。

引用鏈接

1. Arweave Eco Twitter：

https://twitter.com/@ArweaveEco

2. #SPoA：

https://twitter.com/search?q=%23SPoA&src=hashtag_click

3. #SPoRes：

https://twitter.com/search?q=%23SPoRes&src=hashtag_click

4. 原文鏈接：

https://twitter.com/ArweaveOasis/status/1772089247660638417

鄭重聲明：本文版權歸原作者所有，轉載文章僅為傳播信息之目的，不構成任何投資建議，如有侵權行為，請第一時間聯絡我們修改或刪除，多謝。