作者:Steven Yue,原刊於作者知乎
上一期的文章中,我們一起了解了格密碼學到底是什么,隨後我們學習了LWE問題的構造。最後,我們把所學的內容組合起來,構成了格密碼學中最經典的Regev加密算法。(詳情點擊《初探全同態加密:FHE的定義與歷史回顧》)
希望看到這裏,大家已經對上期講到的內容已經有一個深刻的認知了。這一期,我們就可以真正开始實战最後的boss——开始構造全同態加密系統。
上期回顧
在开始之前,爲了便於大家能夠更好理解這期會描述的FHE系統,我們在此快速的復習一下之前兩期文章講到的比較關鍵的知識點。
LWE問題
上期文章中較爲重點的內容就是LWE問題了。可以說正確的理解了LWE,格密碼學和FHE問題就已經搞定了一大半了。

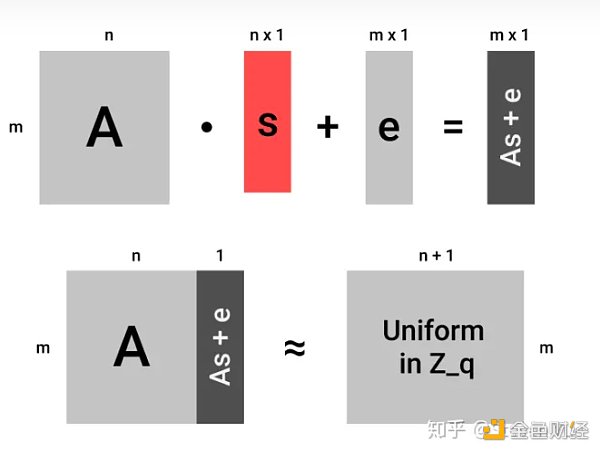




全同態加密體系
最後,我們一起來回顧一下上上期講到的,一個完整的全同態加密(FHE)體系的構造。
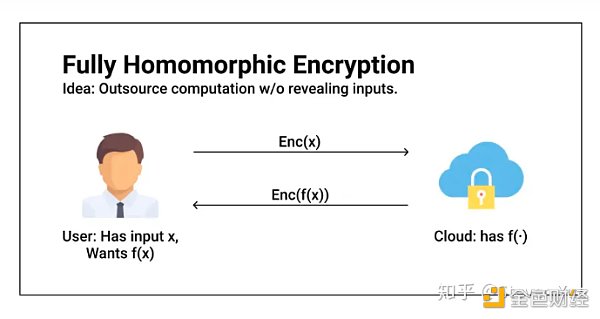


FHE的四個階段
我們在第一期的文章中,還學習了構成FHE系統的四個不同階段:
部分同態(Partially Homomorphic Encryption):在這一階段下,我們可以運算的功能F只能夠要么由加法/线性組合,要么由乘法構成。常見的例子有RSA(乘法同態)以及ElGamal(加法同態)。
近似同態(Somewhat Homomorphic Encryption):這一階段的算法擁有不完整的同態屬性,比如擁有Pairing配對的ElGamal循環群,具有完整的加法同態屬性,但是只有非常薄弱的乘法同態屬性。
有限級數全同態(Leveled Fully Homomorphic Encryption):這一階段的算法可以同態運算任意形式的功能F,但所轉換成的電路的復雜度不能超過上限L,不然就會噪音太大丟失信息。
全同態(Fully Homomorphic Encryption):最後的階段就是我們想要得到的FHE了。在這一階段我們可以計算任意復雜度的功能F,
並且噪音可以被完美的控制在可控範圍內。
我們之前還提到了,通過Bootstrapping的方式,可以有效的將一個有限級數全同態(LFHE)的系統轉換爲一個全同態(FHE)的系統。Bootstrapping這一概念是FHE界的开山鼻祖Craig Gentry在09年的PhD畢業論文中指出的。我們這次要講到的GSW系統,就是一個FLHE系統,隨後通過Bootstrapping被有效的轉換爲FHE系統。
綜上所述,我們這一期來仔細的探討一下,GSW中提出的LFHE系統是怎么構造的吧~
PS:這一段回顧的內容僅僅是前兩期描述的一小部分。所以如果大家看到這裏對FHE的定義與LWE問題還是不夠了解的話,不妨再回去看看之前的文章,然後再回來繼續往下看。
構造GSW-LFHE系統的三次嘗試
GSW系統是Gentry,Sahai,Waters三位大牛在2013年提出的第三代同態加密系統。整套加密系統圍繞了一個核心概念:矩陣的近似特徵向量。
乍一聽,這個概念有點雲裏霧裏的。所以整篇論文其實也分了三個階段,循序漸進的來介紹這一系統的構造。這三個階段中,每一個階段都提出了一個LFHE系統的嘗試,並且評估了這一嘗試是否可行。
話不多說,我們這一期就來詳細的學習一下Gentry在原文中對於LFHE構造的三次嘗試,並且逐步的推導出最後GSW系統的全貌吧。
第一次嘗試:矩陣的特徵值與特徵向量




“加密算法”的問題
我們的第一次嘗試就完美的實現了全同態的所有要求,似乎看上去可以直接收攤,結束這篇文章了。
但是我們不能高興的太早,因爲這一體系有一個非常致命的弱點。如果細心的讀者朋友們會發現,我們在講述第一種方案的時候,一直給“加密”二字打上了引號。

但是這一架構對於我們後續的嘗試是一個很好的啓發,我們缺哪裏補哪裏就行了。上一期的文章中,我們講到高斯消除法可以很好的找到线性方程組的解,但是如果我們疊加了一個噪音的話,就變成了困難的LWE問題。我們這裏不妨也做同樣的嘗試,在特徵向量與特徵值的等式中加入噪音,看看會不會有所變化。










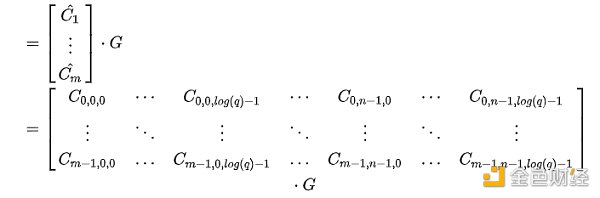








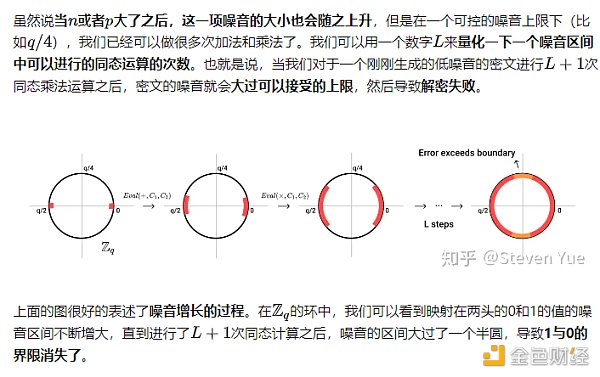

篇尾小結
相比起前兩篇文章來說,這一篇文章可以說是最學術、數學公式最多的了。我盡可能地在描述的過程中用大白話來講述LFHE系統的構造。如果大家在看的過程中還有一些疑惑,不妨把有困惑的地方再讀一遍,或者私信我一起交流!
我在文章开頭有所提到:GSW系統的精華就在於近似特徵向量這么一個定義。我們從普通的特徵向量出發構建了一個全同態、但是不加密的系統;隨後,我們加入了LWE問題中類似的噪音向量,構成了一個部分同態、但加密的系統。最後,我們使用二進制分解這么一個工具,構成了GSW中最後提到的有限級數全同態加密系統。
看到這兒,如果你已經能get到GSW系統在做什么,是怎么來的的話,恭喜你已經掌握FHE系統構造的精髓啦!這是一件值得高興的事情,因爲FHE是一個相對來說非常年輕(~10年)的領域,我們已經站在密碼學技術很前沿了。
下一步,是什么?
我們現在已經根據GSW這一篇paper所述的,一起構建出了一套LFHE系統了。但是就像我在第一篇中承諾的——我們要再接再厲,衝向真正的FHE。
(注:GSW的paper中講到的加密算法和我們本文中提到的可能有所出入,使用的是一種非對稱的形式,而我們用的是對稱加密形式。但是這並不會影響整個體系的正確性或者是功能性。個人覺得這樣更好理解一點。)
爲了能夠把LFHE系統轉換爲真正的FHE系統,我們就需要用到Gentry大佬提出來的Bootstrapping這一方法了。簡單的來說,Bootstrapping可以把一個即將達到臨界值的、帶有很大噪音的密文,”刷新“成一個噪音很小的密文,這樣就可以無限制的進行同態運算了。
下一期,我們詳細的介紹一下GSW系統中是如何應用Bootstrapping把原本的LFHE轉換爲FHE的。篇幅允許的話,我們還可以來探討一下現有FHE庫(如HELib,SEAL,TFHE)等的區別。下期見啦~
鄭重聲明:本文版權歸原作者所有,轉載文章僅為傳播信息之目的,不構成任何投資建議,如有侵權行為,請第一時間聯絡我們修改或刪除,多謝。
